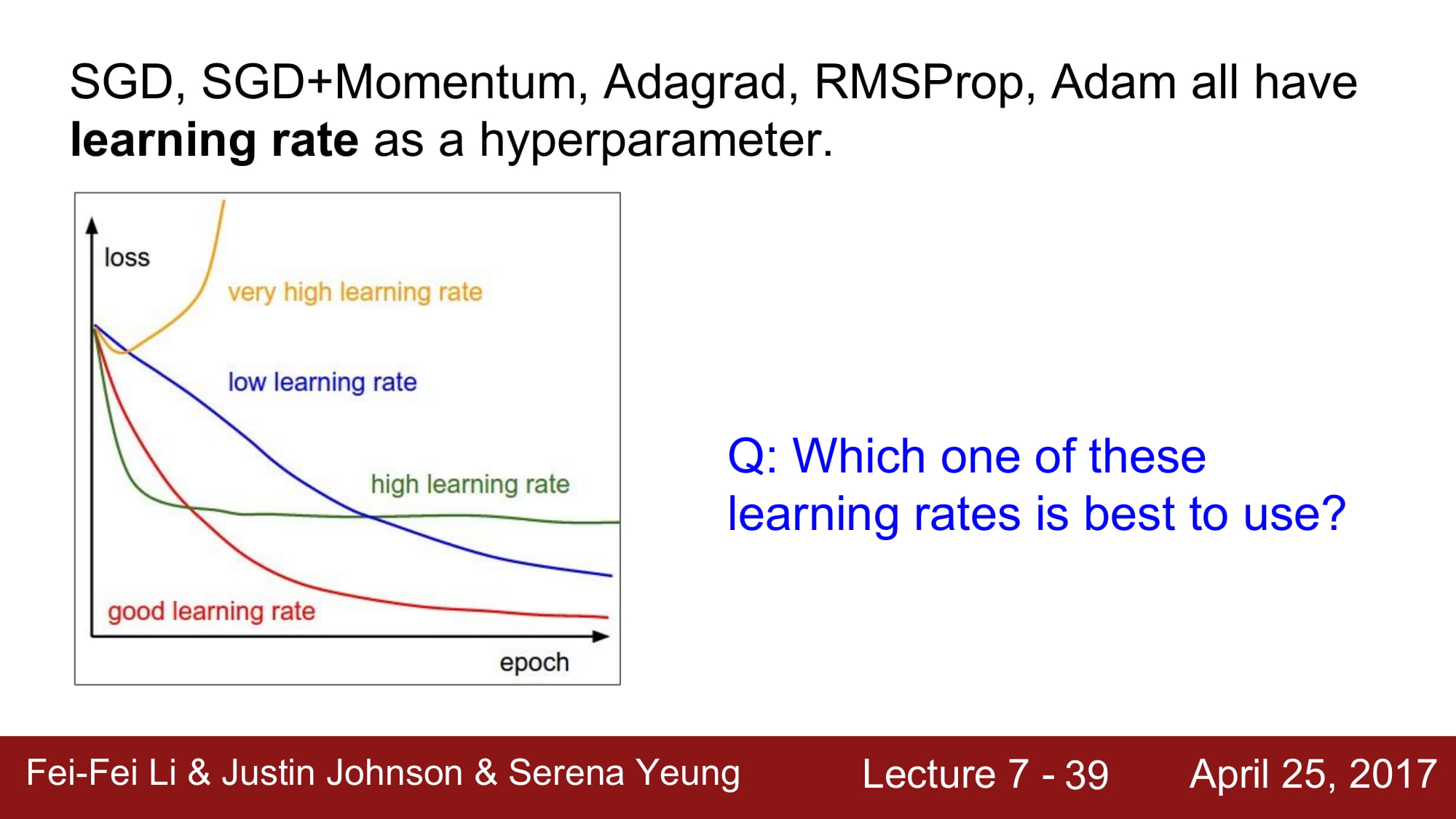
모든 Optimizer 들은 learning rate 을 parameter 로 가진다.
위 그래프는 항상 많이 보았던 learning rate 를 ‘적절히’ 잘 줘야한다는 걸 설명하는 그래프 이다.
그럼 하나의 learning rate 을 static 하게 learning 이 끝날때 까지 유지해야하는건가? 아니다!
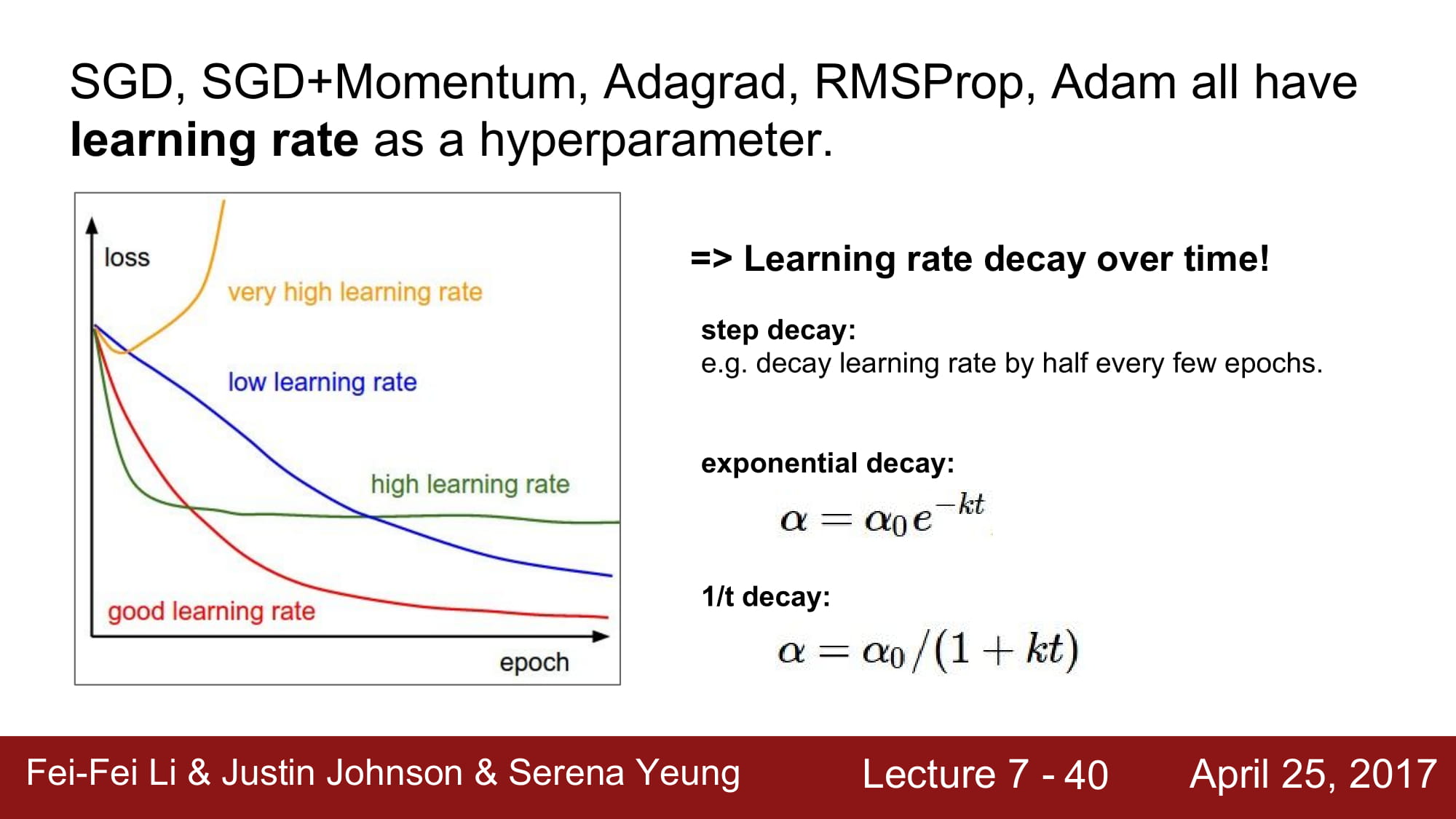
learning rate decay 라는 방식이 있다.
통칭 Annealing learning rate 기법중 하나로, step decay, exponential decay, 1/t decay 방식이 있다.
- Step decay 는 몇 Epoch 마다 일정량만큼 학습 속도를 줄이는 방식이다.
- exponential decay 는 위 수식처럼 a_0, k 라는 hyper parameter 를 가진다. t 는 반복 횟수이다.
- 1/t decay 또한 a_0, k 라는 hyper parameter 를 가진다. t 는 반복 횟수이다.
실제로는 step decay가 많이 사용된다.
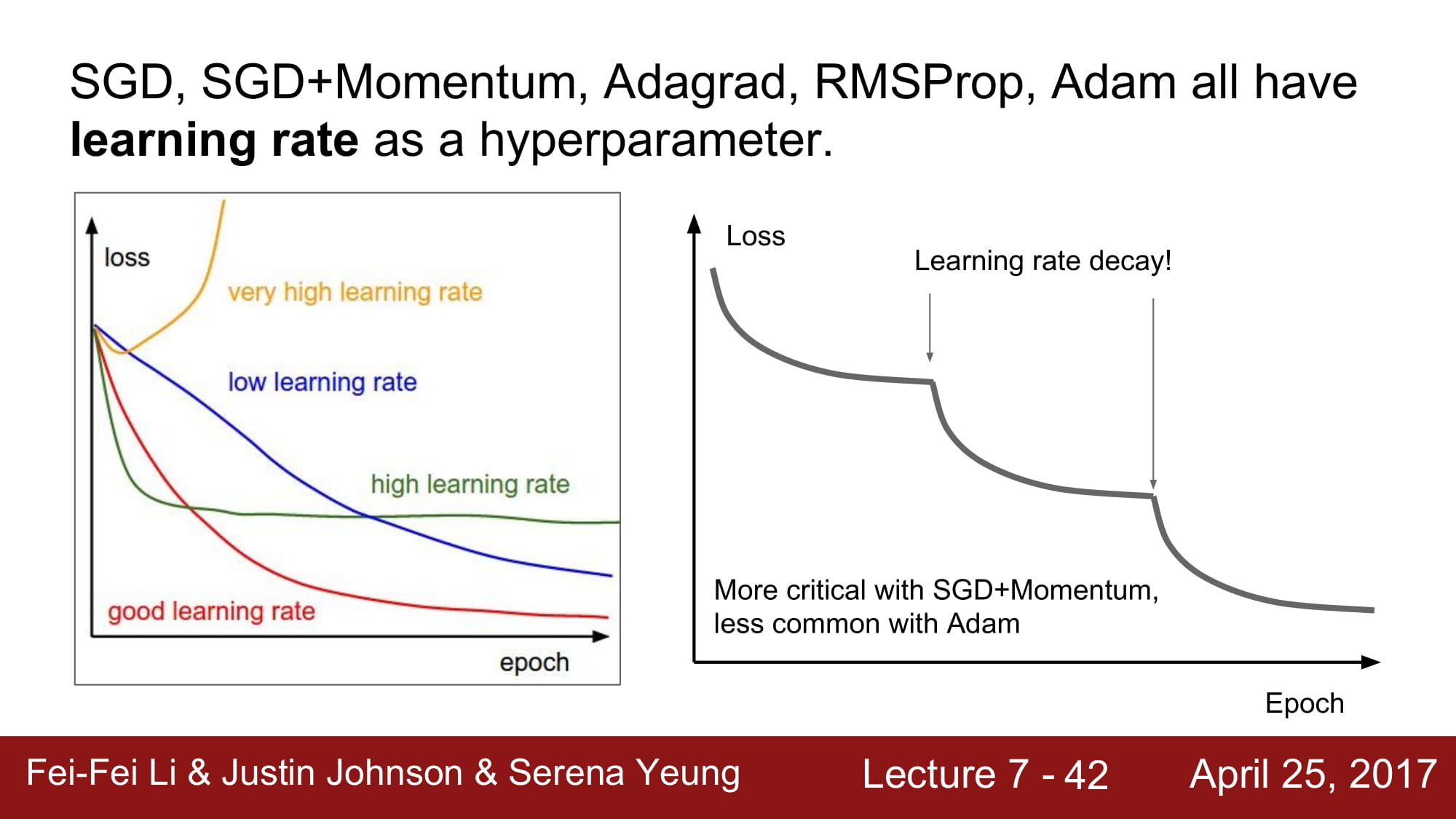
특정 learning rate 으로는 general 하게 올수 있는 한계가 온다. 그래프에서 점차 평탄해지는 구간이 있는것을 알 수 있다. 이때 learning rate decay 가 들어가게 되면, general 한 상태에서는 학습할 수 없었던 구간까지 학습할 수 있는 효과를 가진다.
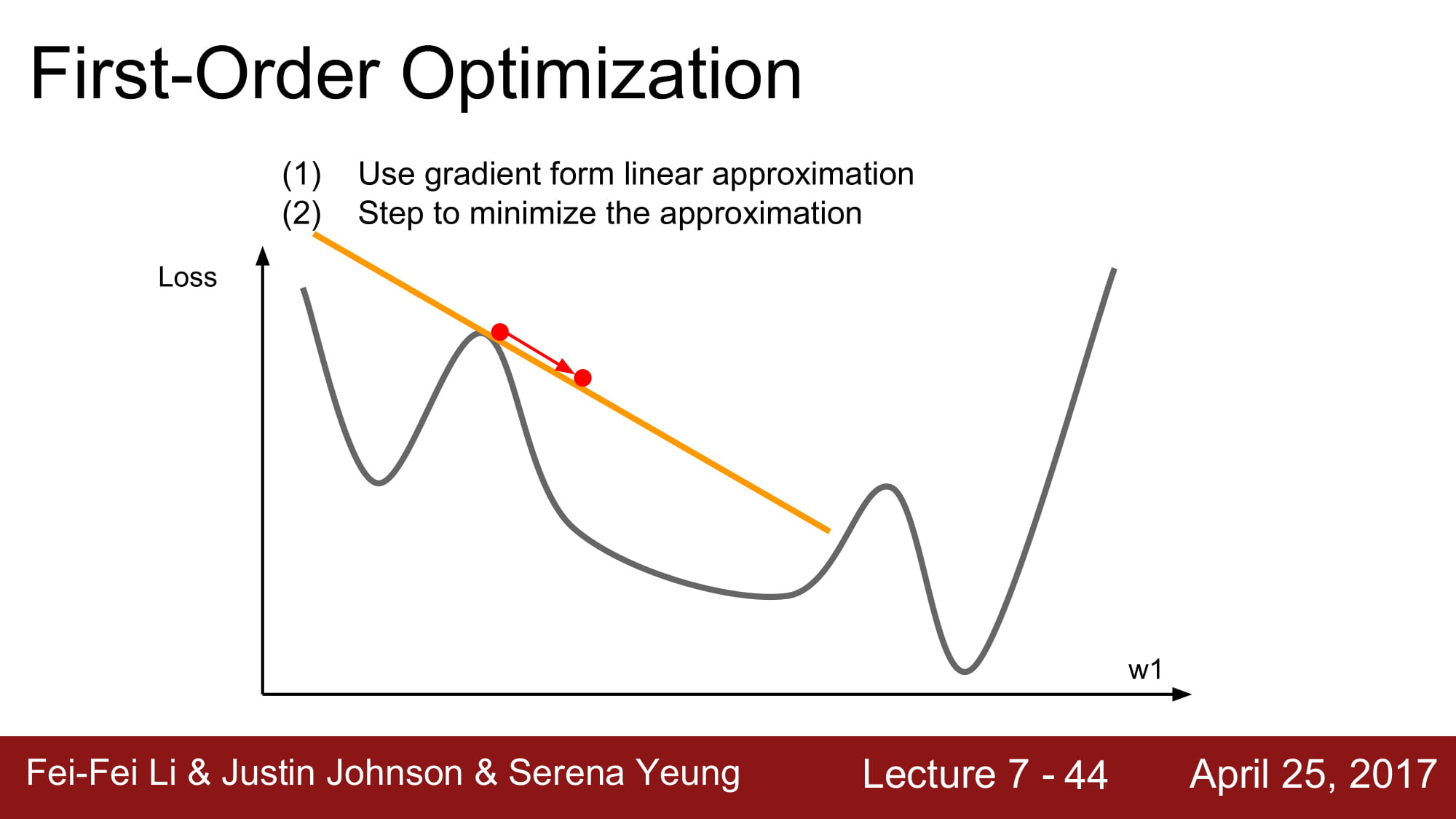
지금까지 배웠던것은 first order optimization 이다!
minimize 를 가기 위해 step 을 밟아가며 여러번의 linear approximation을 반복하며 계단을 하나하나 걸어가는 모습을 보였다.
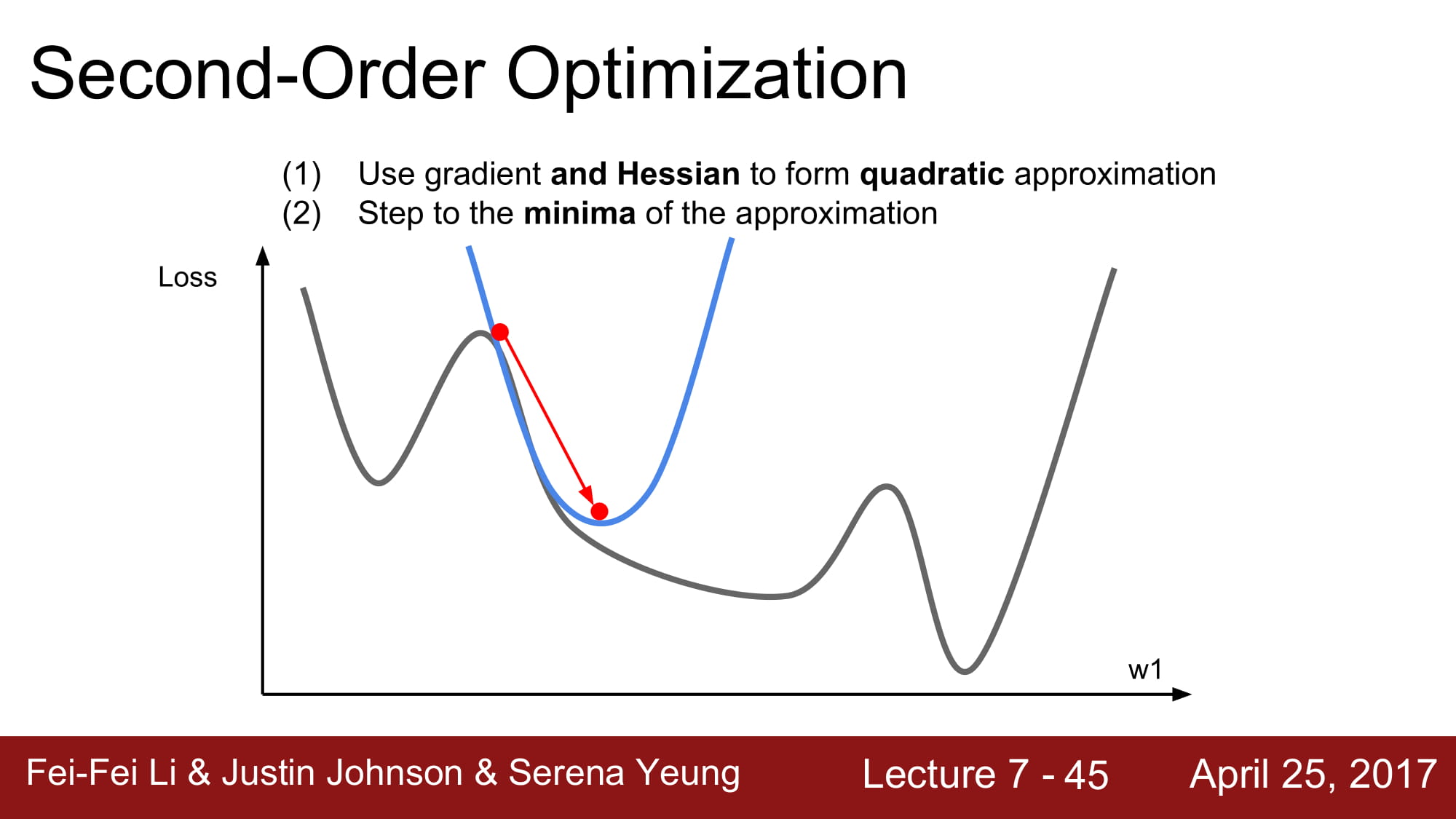
이와 다르게 Second order optimization 이란것도 있다. 사실 이 파트는 이해하기 매우 어렵다. 이 수학에 대해서도 따로 한번 정리해서 한 주동안은 수학만 해야할 것 같다.
내가 이해한 정도로는, 2차 근사를 통해 어떤 함수의 local curvature를 알아내어 곡률이 약한 방향으로 더 많이 업데이트를, 곡률이 강한 방향으로는 적게 업데이트를 수식적으로 ‘알아서’ 할 수 있게 된다.

second-order optimization 에는 Newton’s method 가 나오는데, 여기서 테일러 급수가 등장한다.
대략 여기서부터 머리에서 과부하가 걸리기 시작했다.
일단 헤시안 metrix 를 통해서 극대와 극소를 알 수 있는것은 알겠는데… 그 다음부터는 너무 수학수학하다.
뉴턴 방법은 뭐고 테일러급수는 대학때 확통과 이산수학, 선형대수만 배웠어서(사실 이거도 충분하지 않다) 너무 생소하다.
태일러 급수와 뉴턴 방법, 헤시안 행렬 등을 공부하기 위해서 다음주는 미적분을 공부해야겠다.

No hypeparameter! No learning rate! 정말 놀랍다!
근데 왜 지금은 안쓰는 방법일까??

Hessain metrix 를 구하는데 N^2, 역행렬 구하는데 N^3 이 걸린다.
대략 정신이 혼미해진다. N 은 수백만인데 여기서 제곱에 세제곱?
컴퓨팅 파워가 너무 많이 들어서 못쓰는것이였다.

Hessain metrix 의 역행렬을 구할때 완벽히 구하지 않고 역행렬을 근사하는 방식도 있다고 한다. BGFS 라고 하는거같다.
L-BFGS 는 시간에 따른 gradient 의 변화를 근사하는 방식을 사용한다.
그럼 뭔가 다 L-BFGS 를 쓰면 해결될 거같지만.. 또 큰 문제가 있다.
L-BFGS 는 mini-batch 를 사용하지 못한다는것이다. L-BFGS 알고리즘에 mini-batch 를 녹이는 것은 아직 한창 연구중이라고 한다.


결론
Adam 쓰면 된다.