
11장은 Classfication 이 외에 비전 분야에서 유명한 다른 문제들을 소개하고, 대표 모델들을 학습합니다.
또한 Multi Loss 와 Region Proposlas, downsampling, upSampling 등을 학습합니다.
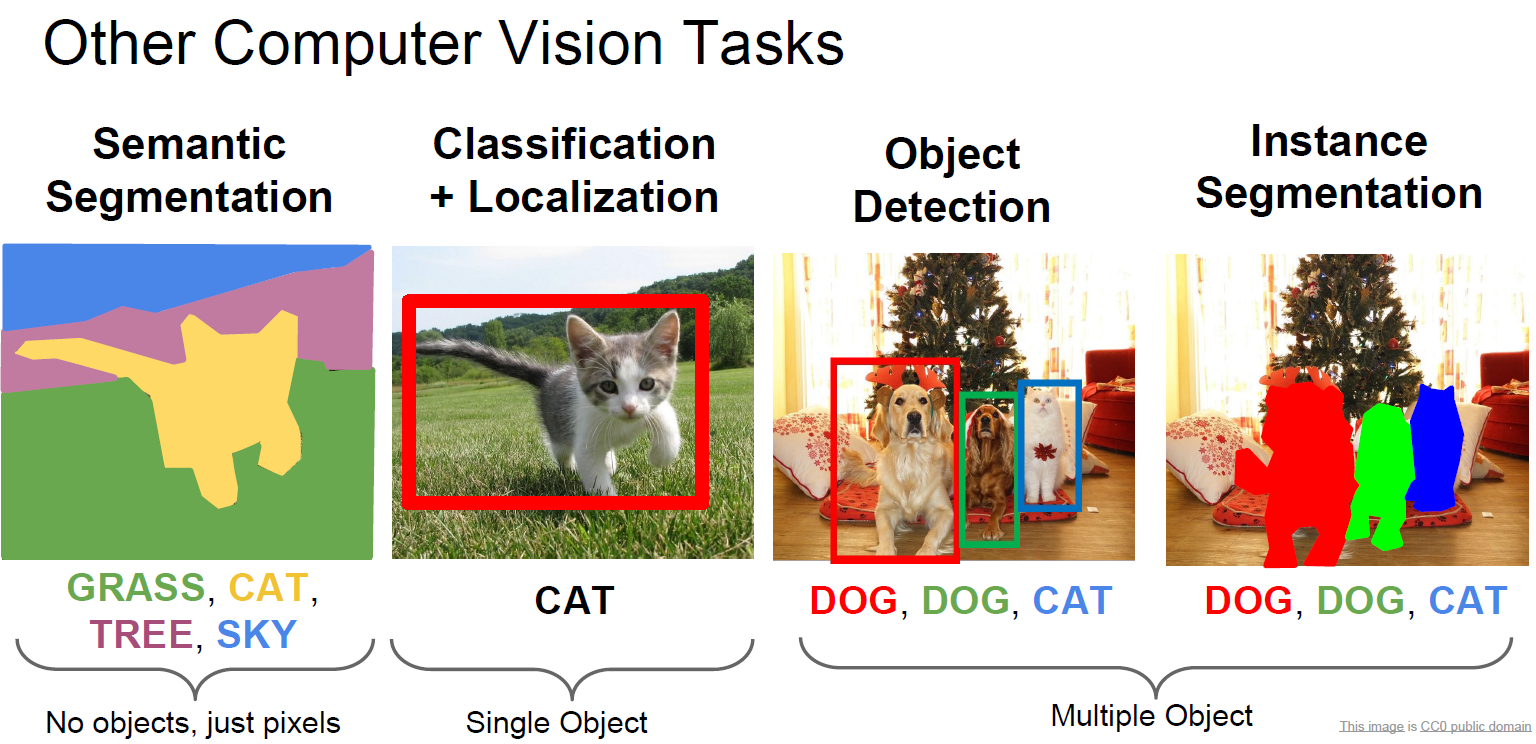
기본적으로 배운 Classification
그 외에도 Segmentation, Object Detection 등이 있고 두 개의 발전 모델인 instance Segmentation 등이 있습니다.
이제 하나하나 학습해봅시다.
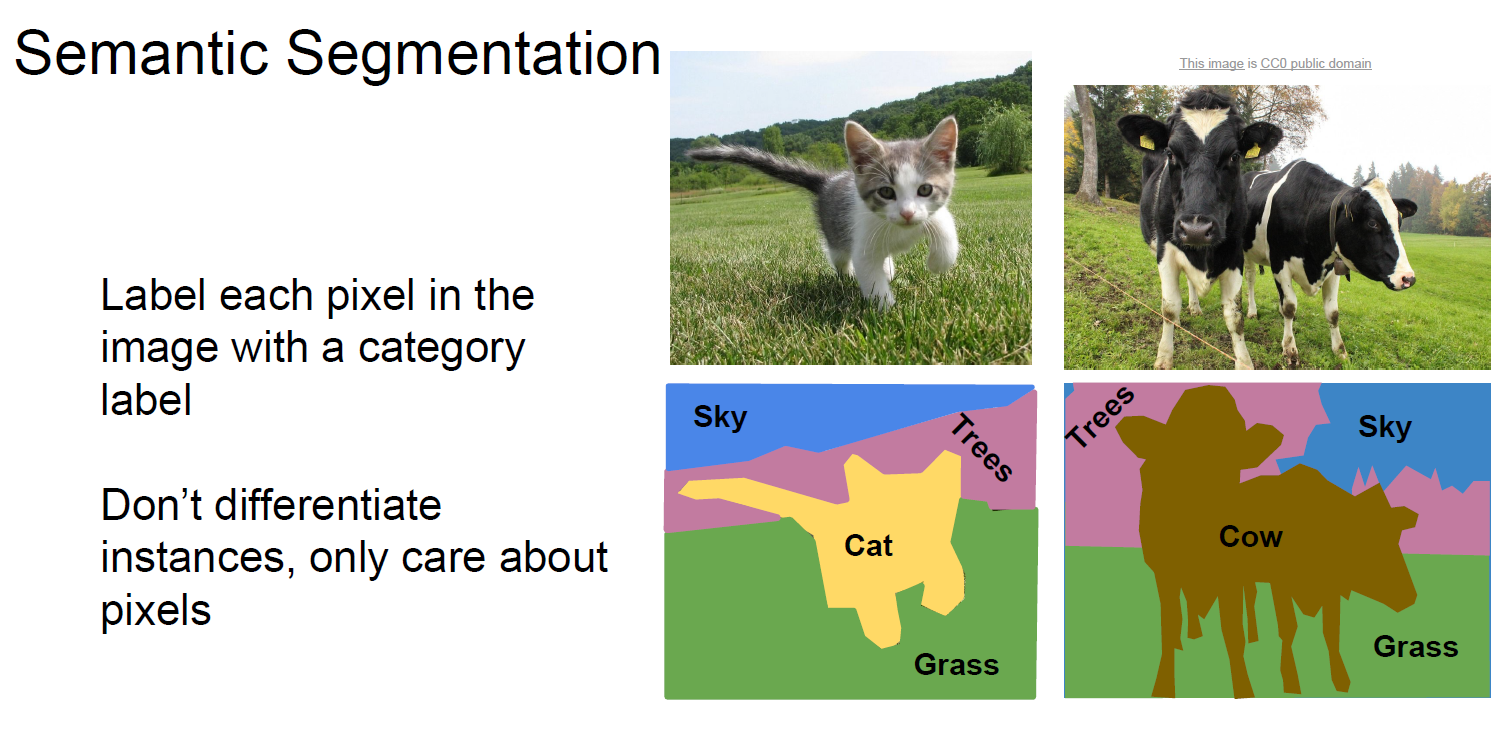
Semantic Segmentation은 Pixel에 Label 을 붙이는 작업 입니다.
어떻게 Segmentation 문제를 풀까요?
일단 기본적으로 생각나는 Sliding Window 부터 생각해봅시다.
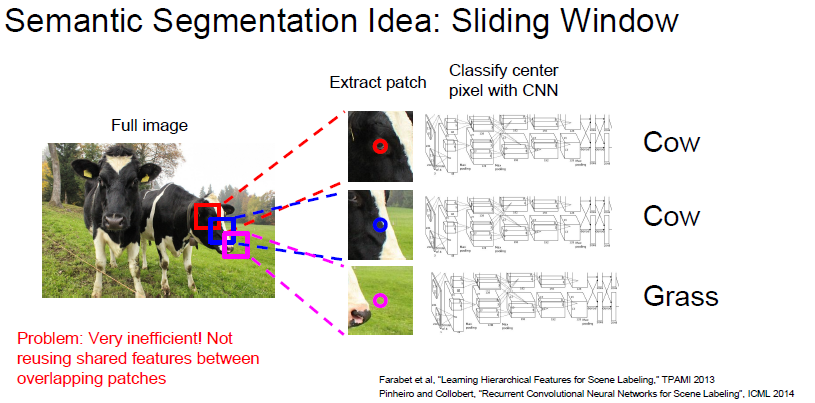
일단 Sliding window 하면서 각각 뽑힌 patch 들을 CNN 으로 분류한다고 생각해봅시다.
일단 Computational cost 가 굉장히 크고, feature 들을 서로 공유하지않아 중복 연산이 매우 많게됩니다.
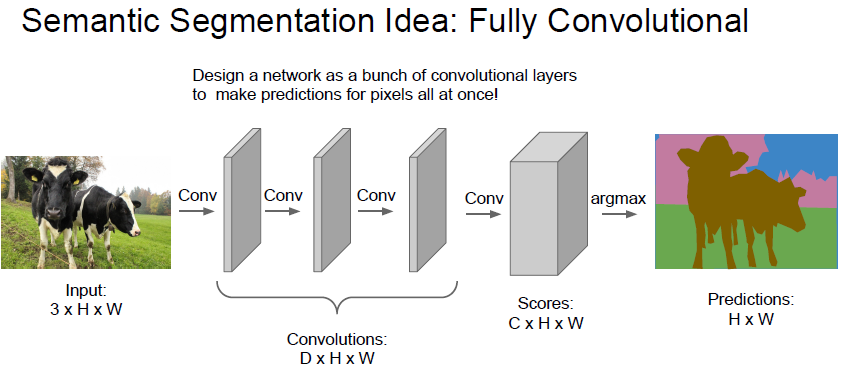
두 번째 아이디어는 Fully Convolutional 이라는 아이디어인데,
3 channel 로 이루어지고 크기가 H x W 인 이미지가 있다면, 여기서 Conv layer를 거치면서
원본 이미지와 크기가 같은 Convolution 을 계속 거치게 되는것입니다.
최종적으로 C 개의 Class 가 있다면, Convolution 의 결과는 C x H x W
즉 각 pixel 별로 해당 pixel 이 각각 어느 Class 인지 정보를 Pixel 단위로 학습하는것입니다.
하지만 원본 이미지만큼의 Convolution은 매우매우 computational cost 가 비쌉니다.
학습 전 어떻게 데이터 전처리를 해두어야하나? 정말 pixel 단위로 Class 를 레이블링 해둬야하나????
맞다. Pixel 별로 Class 를 레이블링 해두어야 학습 할 수 있다.
전처리가 매우 빡세다.
일단 Conv layer 를 저렇게 활용하는것보다, Data 를 압축시켜서 러닝 시키자! 라는 아이디어가 있었다
이게 바로 downsampling 과 upsampling 의 등장 배경이다.
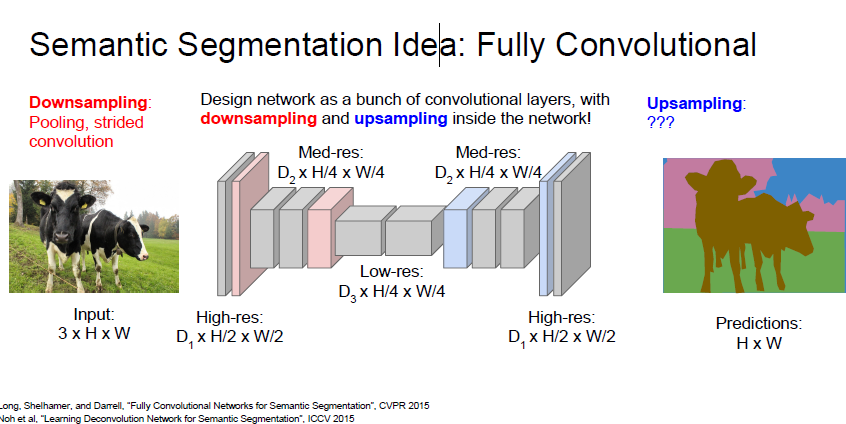
위와 같은 U 자 네트워크를 통해서 feature 를 뽑아 낸 후, 해당 feature를 다시 upsampling 하는 형식으로 학습한다고 합니다.
근데 여기서 잠시 생각해보면
downsampling 의 경우 strided Convolution과 Pooling layer 를 통해 충분히 가능하겠지만
그럼 upsampling 은 어떻게 하는걸까요?
이제 알아봅시다.
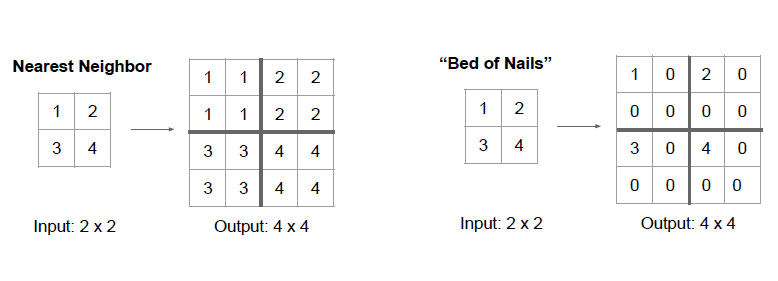
Nearest Neighbor 는 down sampling 되어있는 feature 를 복사해서 늘리는 방식입니다.
만약 크기가 가로 새로로 2배 늘어난다면, 그 값을 복사해서 주변에 넣는 방식입니다.
Bed of Nails 방식은 1번 위치에 해당 값을 넣고 남은 자리는 0으로 채우는 방식입니다.
해당 영역에서 자신만 혼자 튀어나와있어서 Bed of Nails 라고 부른다하네요
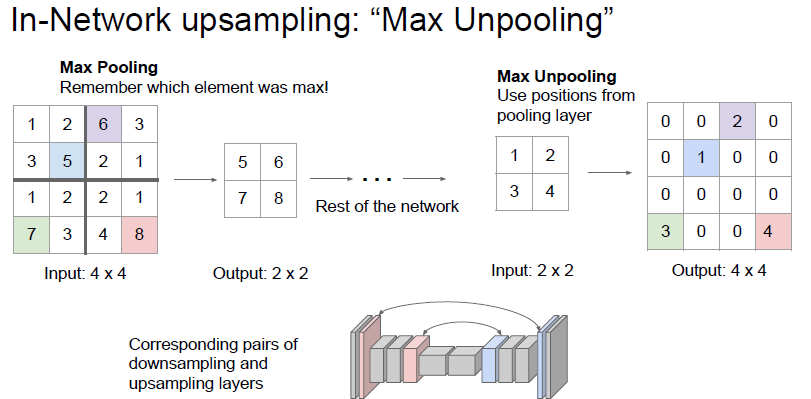
다음으로 max Unpooling 이라는 방식이 있습니다.
이전 downsampling 할때 max pooling 한 자리를 기억해두었다가 max unpooling 할 때 다시 그 자리로 값 을 넣고 upsampling 하는 방식입니다.
max pooling 으로 잃는 공간 정보를 max unpooling 으로 다시 일부 회복할 수 있다고 합니다.
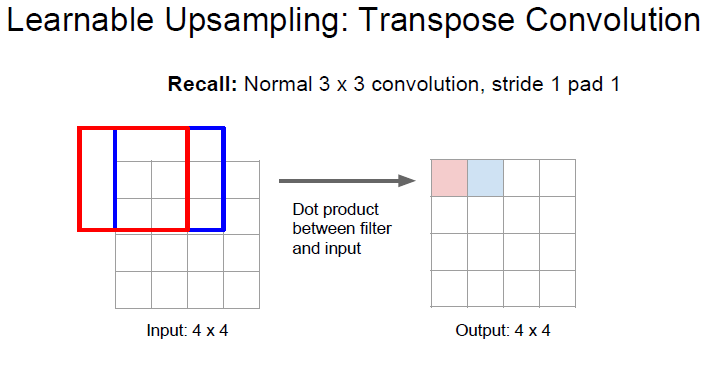
지금까지는 Pooling layer 이였기 때문에 학습할 수 있는 파라미터가 없었습니다.
이제 down sampling 에 있던 2가지 요소중 하나인 Convolution layer 를 upsampling 에도 가져와봅시다.
stride 가 1 인 상태에서 convolution 하게되면 위와같은 결과가 나오게 됩니다.
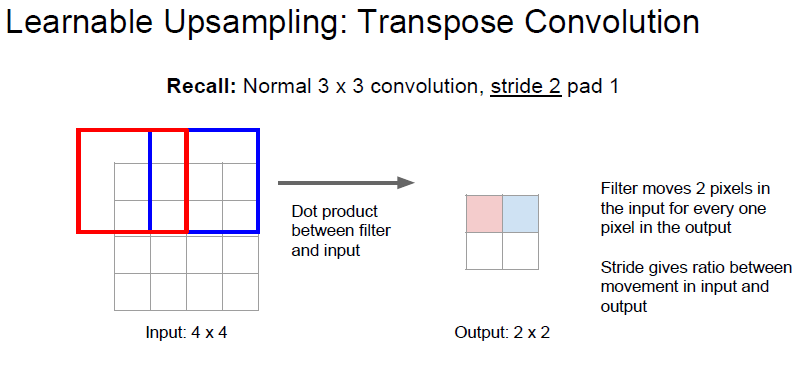
stride 가 2 인 상태에서 convolution 하게된다면 위와같이 down sampling 되게 됩니다.
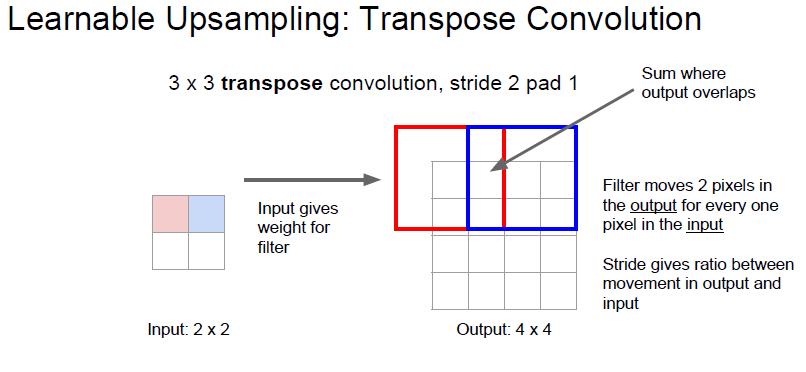
Transpose Convolution 은 위의 Convolution 을 반대로 한것입니다.
filter가 input matrix 에서 움직이는것이 아닌 output matrix 에서 움직이게 하는것입니다.
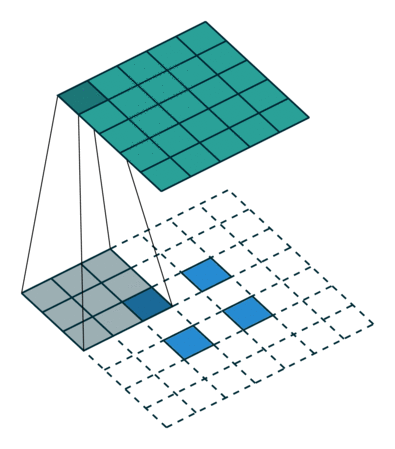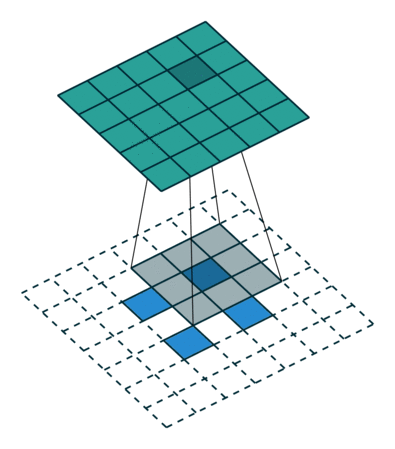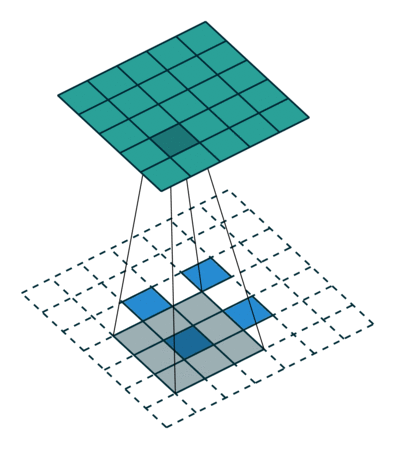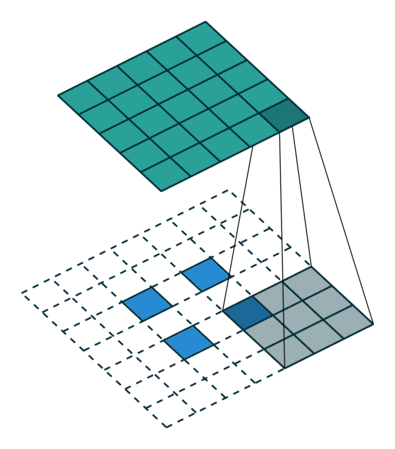
우리가 원하는 transpose convolution 은 위와같은 연산입니다.
행렬의 하나 하나 원소들을 filter 를 거쳐서 matrix 의 일부분에 투영 시키는 것이죠.
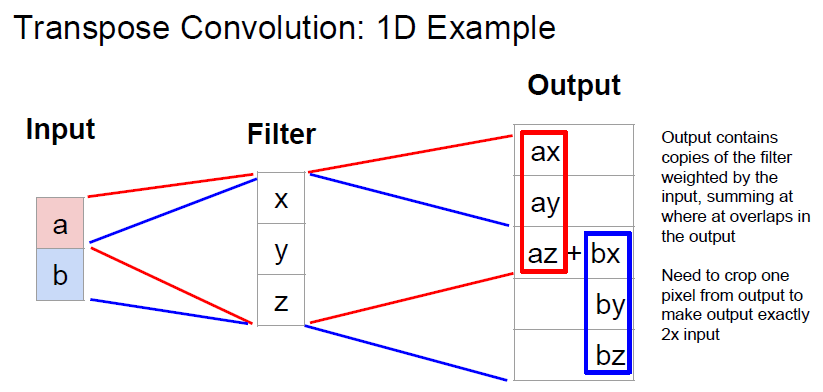
조금 더 예시를 보면
[x,y,z]T 라는 filter 가 있다면, input 과 filter 를 곱하여 output 에 붙여넣게 됩니다.
사실 위의 그림을 보면, 왜 처음에 ouput matrix 위에서 움직이게 하지? 라는 생각이 들기는합니다.
여기서 위 연산을 2가지 관점으로 생각 할 수 있는데 다음과 같습니다.
- input 에 filter 를 적용하는것이 아닌 output 에 filter 를 적용한다
- input 에 filter 를 적용하는대신 filter 를 transpose 해서 곱한다
사실 두 관점이 같은걸 말하는것입니다.
그래서 사람들이 deconvolution 이라는 말로도 표현하고, transpose convolution 이라는 말로도 표현한다고 합니다.
하지만 실제로 deconvolution 을 하는게 아니므로 transpose convolution 이 맞는 표현이라고 합니다.
deconvolution 이 해야하는 연산은 convolutoin 의 결과를 되돌리는 역활입니다. 수식적으로 역산을 하는것이죠.
하지만 위의 연산은 그게 아니죠. upsampling 을 위해 사용하는것이니까요.
Matrix multiplication 영역에서 Convolution 연산을 살펴봅시다.

1D Convolution 에서 filter 의 움직임을 위와같이 matrix 로 표현할 수 있습니다.
upsampling 에서는 오른쪽과같이 matrix 가 형성된다고 합니다.
잘 보면 왼쪽 stride 1 convolution 의 filter를 transpose 시키면 오른쪽의 filter 가 됩니다.
일반적인 filter 를 사용하는 convolution 이랑 비슷해보입니다.
하지만 stride 가 2 이상이라면 상황은 달라집니다.

stride 가 2 이상이 되면, 일반적인 Convolution 과 달라진다고 합니다.
음.. 이건 왜 그런지 잘 모르겠네요..
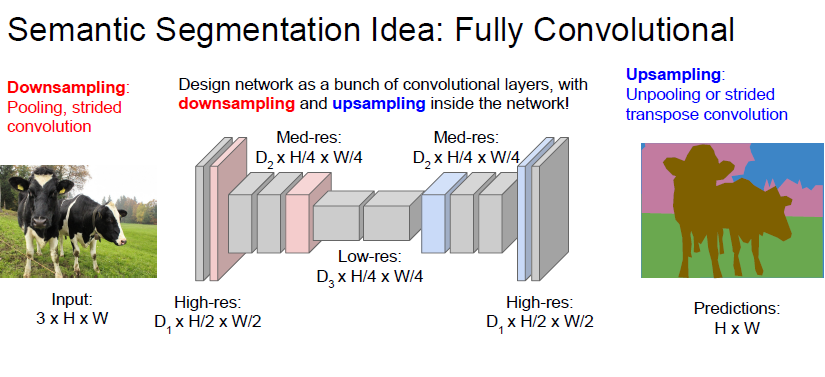
주로 Semantic Segmentation 은 위와같은 구조를 가진다 합니다.
down-sampling 과 upsampling 을 통해 각 pixel 에 대해 Cross-entrorpy 를 통해 class 를 prediction 한다고 합니다. Loss 는 마지막 layer 로 부터 흘릴 수 있기 때문에 End2End 학습이 가능하다고 합니다.