5.1, 2, 3 Decision Boundary with Margin, Maximizing the Margin, SVM with Matlab

Files: https://strutive07.github.io/assets/images/5_1_2_3_Decision_Boundary_with_Margin_Maximizing_t/IE661-Week_5-Part_1-icmoon-ver-1.pdf last update datetime: Jan 21, 2020 11:00 PM

Decision boundary는 classification에서 가장 중요한 요소이다.

앞에서 배웠던 logistic regression, naive bayes를 확률과 연관지어서 생각했다. 한번 확률을 빼고 생각해보자.

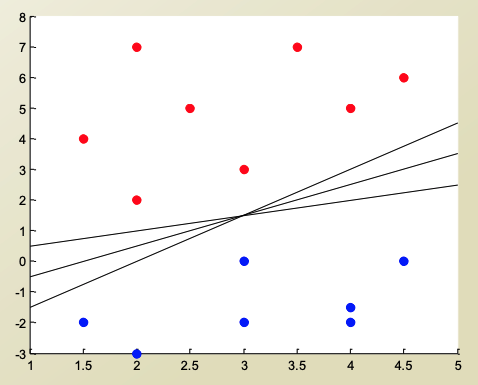
이러한 데이터가 있다고 가정해보자.

Decision boundary는 빨강색과 파랑색을 명확하게 구분지을 수 있는 boundary를 가지고 있어야한다.

위의 그림처럼 여러가지 후보의 선형 decision bondary가 나올 수 있다.

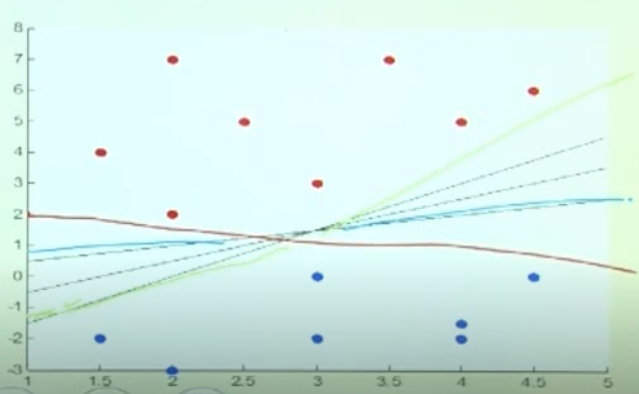
빨강 파랑 연두 decision boundary중 어떤것이 가장 좋은 decision bondary 일까?

파랑색이다.

그냥 일반적으로 생각해보자. 데이터중 decision boundary와 가장 가까운 node의 거리가 작아질수록, error에 약할것이다. 따라서 파랑색 선 같이 최대한 node들과 멀어진 decision boundary가 좋은것이다.

이를 조금 더 수학적으로 생각해보자.

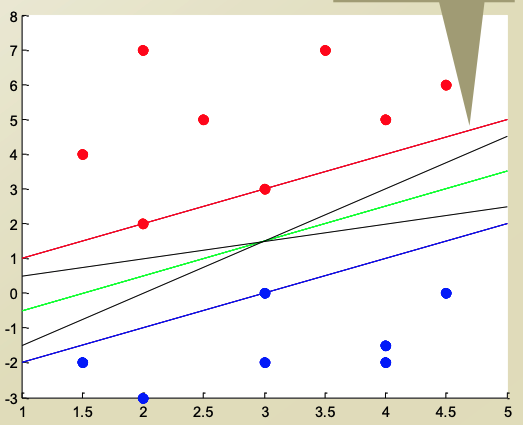
빨강색 class의 최남단을 나타내는 선 하나와, 파랑색 class의 최북단을 나타내는 선 하나가 있다고 가정해보자.

이 두 선이 평행하다라고 한다면, decision boundary를 키우는 방법은 이 두 선 사이의 거리가 멀어지도록 조정하는것이 된다.

여기서는 decision boundary를 이 두 선의 중앙값으로 잡고있다.(연두색선)

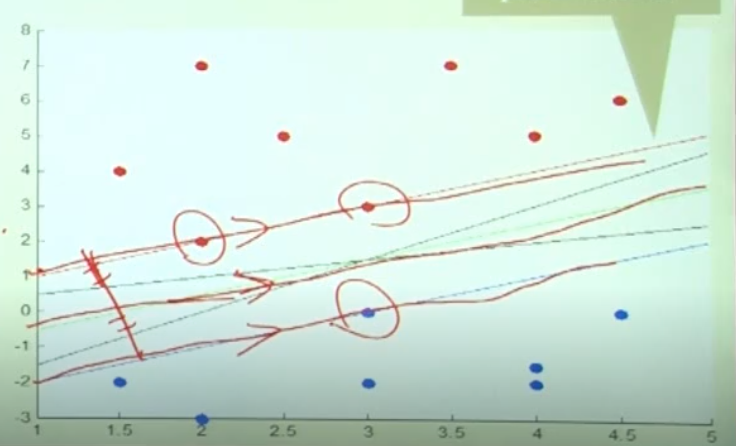
그러면 우리에게 가장 중요한것은, 어느 vector를 기준으로 이 평행선을 만들것인가? 이다. support vector machine의 이름의 이유이기도 하다. 이 vector들을 support vector라고 부르기 때문이다.

이 decision boundary를 wx + b = 0 형태로 나타내보자.

$$f(x) = wx+b$$

여기서 2차원 공간 이므로, w 는 2개의 parameter를, bias 는 1개의 paremter를 가진다.

여기서 w는 decision boundary의 법선 벡터이고, b는 bias 이다.

파랑색을 wx+b > 0, positive라고 가정하고(면 위에 있음),

$$f(x) = wx+b = a, a>0$$

빨강색을 wx+b < 0, negative라고 가정하고(면 밑에 있음) 라고 가정해보자.

$$f(x) = wx+b = a, a < 0$$

그리고 decision boundary에 딱 걸쳐있는 Node는 0을 반환한다.

$$f(x) = wx+b = a, a = 0$$

positive일때 y를 +1, negative일때 y를 -1 이라고 해보자.

• Confidence level(score)

$$(wx_i + b)y_i\space은\space항상\space양수가\space된다.$$

결국 각 class에 대한 신뢰도 점수(confidence score)는 얼마나 이 decision bondary를 믿을 수 있는가? 에 대한 score가 되고, 이 값을 최대화 좋은 decision boundary를 얻을 수 있을것이다.

• Margin

margin은 decision boundary와 node 사이를 말한다.

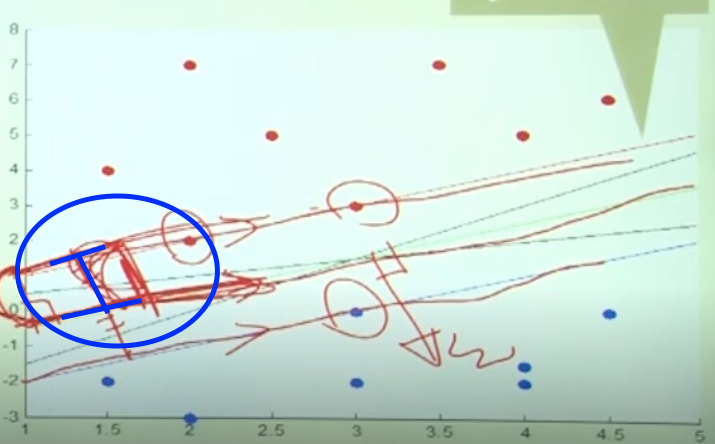
Margin distance

margin distance은 decision boundary와 각 class의 가장 가까운 node와의 거리를 의미한다. 결국 좋은 SVMd을 만들기 위해서는 이 margin distance를 최대화하면 될것이다.

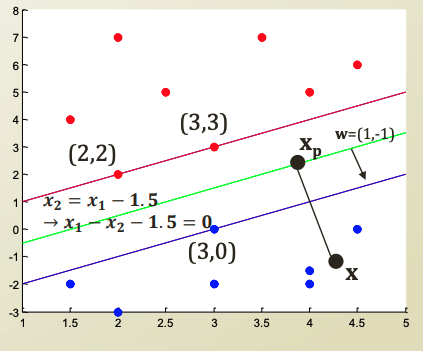
특점 지점 x와 decision boundary와의 거리는, x에서 decision boundary까지의 perpendicular line을 긋고, 그 길이만큼이 될것이다. (고등 수학에서 배운 수선 이다. x_p 는 그럼 수선의 발 이 될것이다)

x에서 xp 까지의 거리가 곳 x와 decision boundary까지의 거리이다.

계속 고등 수학을 응용해보자.

$$x = x_p + r \cfrac{w}{\Vert w \Vert}, f(x_p) - 0$$

x의 거리를 x_p로 나타낸다면, x_p에서 우리가 구할 길이 r만큼을 수선의 방향으로 이동한것일것이다.

그리고 x_p는 decision bondary에서 0이다.

$$f(x) = wx+b = w(x_p + r \cfrac{w}{\Vert w \Vert} ) + b = wx_p + b + r \cfrac{ww}{\Vert w \Vert}$$

여기서 wx_p + b는 0 이므로, 식을 전개할 수 있다.

$$f(x) = r\Vert w \Vert, r = \cfrac{f(x)}{\Vert w \Vert}$$

distance r을 최대화 하기 위해서는, 위 식을 최대화 하면될것이다. 여기서 우리가 건드려야하는 파라미터는 w, b 가 있다. 이를 수식으로 표현해보자.

$$max_{w,b} 2r = \cfrac{2f(x)}{\Vert w \Vert}$$

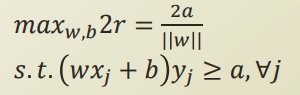
식을 a 라는 임의의 상수로 바꿔서 식을 전개해보자.

그럼 결국

W

를 optimize해야하는데, 일단 이 식을 풀면 다음과같이 square term이 된다.

$$\sqrt{w_1^2 + w_2^2}$$

sqrt같은경우는 단조증가하는 function이기때문에 optimize할때 제외한다고 생각해보자. 결국 우리는 square term을 최적화해야한다.

이럴때는 linear programming, quadratic programming … 등등의 최적화 기법을 사용하여 최적화할 수 있다.

이 최적화방법들은 gradient descent/ascent 같이 한 슬라이드에 설명하긴 어려우므로 나중에 혼자서 찾아봐야함. 이번 강의에서는 커버 X

Support Vector Machine with hard margin

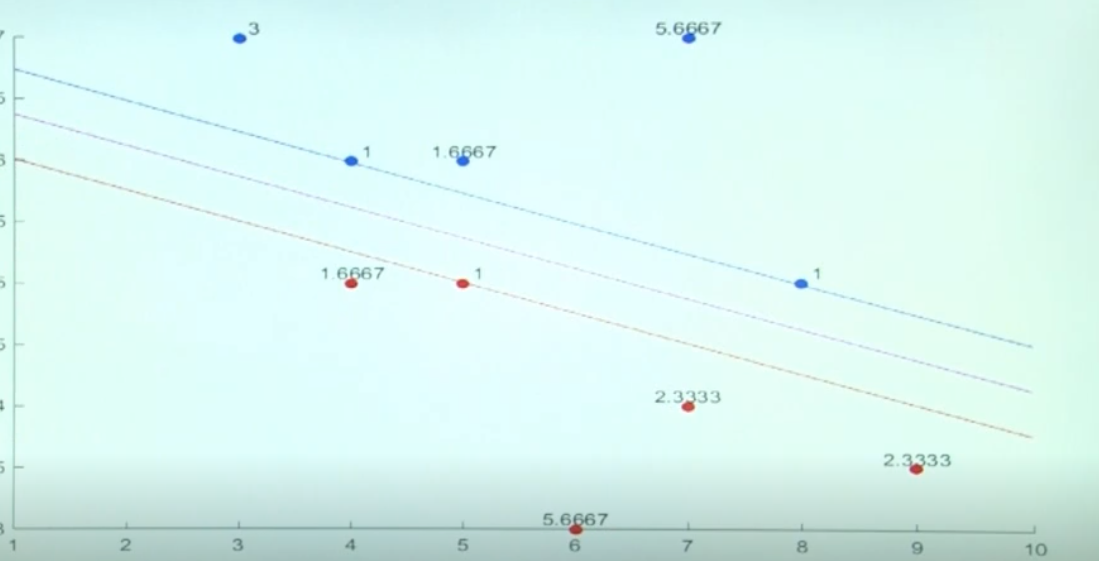
Data가 nice하게, error가 없이 주어진 상황이라면, 위와같이 decision boundary가 이쁘게 형성될것이다.

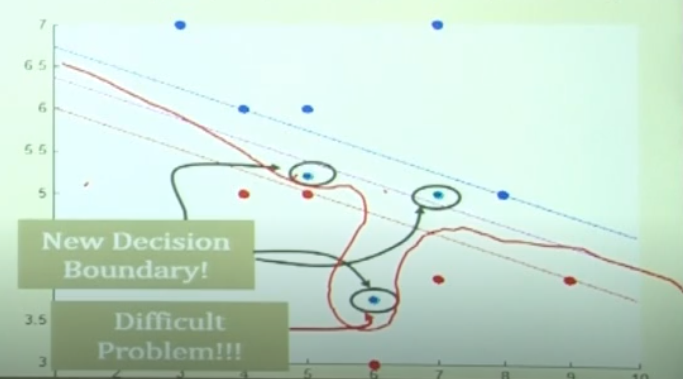
하지만, 현실에서는 항상 noise가 존재한다. 만약 빨강색 영역에 하나의 파랑색 node가 존재하면 decision boundary가 어떻게 형성이 될까??

이런 문제가 생긴다.

hard margin 을 적용했을때 조금의 noise만 존재하면 decision boundary가 이상하게 형성된다.

이는 최적화 문제에서 ‘no fesible solution’ 인 상태이다. 최적해를 구할 수 없는 상황인것이다.

• hard margin

hard margin이란, SVM의 결과에서 하나의 에러도 허용하지 않는 상태를 말한다.

hard margin인 상태에서, 모든 case를 커버하기 위해서는 kernel trick이란것이 필요하다. 이것은 다음 강의에서 설명할 예정.