Files: https://strutive07.github.io/assets/images/5_4_Error_Handling_in_SVM/IE661-Week_5-Part_2-icmoon-ver-1.pdf last update datetime: Jan 27, 2020 1:09 PM
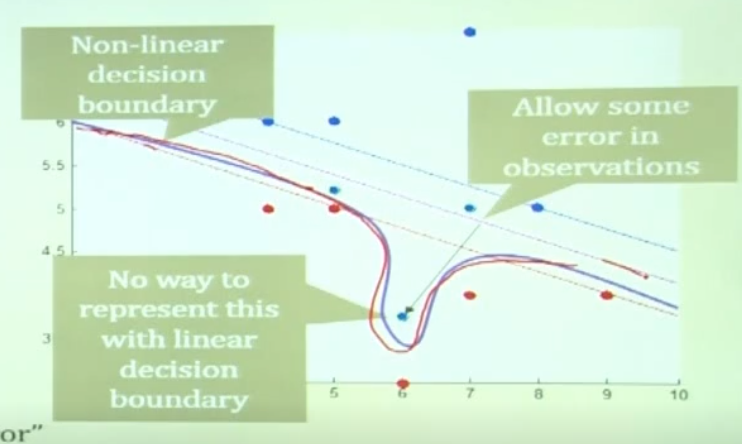
이렇게 데이터에 noise가 있는 상태에서, 어떻게하면 decision boundary를 잘 찾을 수 있을까?
- 위 그림처럼 non linear decision boundary를 생성하는 방법이 있을수도 있고,
- 아니면 이런 noise를 무시하고 decision boundary를 생성하는 방법도 있다.
- 또한, 거리에 따른 반칙 스코어를 주어서 그 스코어를 최소화 하도록 최적화를 하는 방식도 있다.
이번엔 세 번째 방법을 한번 공부해보자.
Error handling in SVM
- option 1
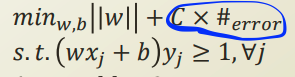
기존의 quadratic programming을 통해 최적화를 하던 식에 panalty를 주는것이다.
Loss function
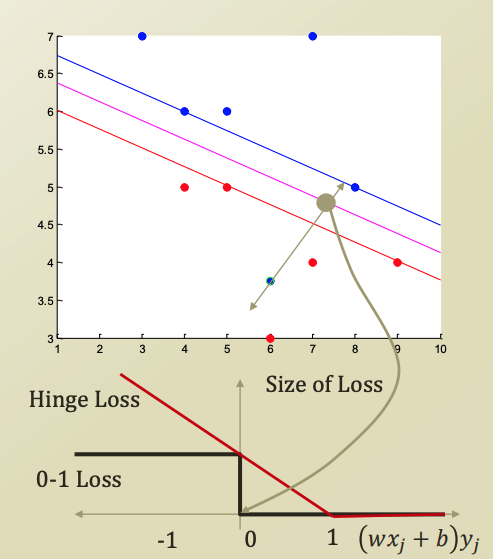
우리는 SVM 식을 유도할때, a 라는 margin을 가정하고 식을 구성했다. a는 decision boundary로부터 class 의 평행선 까지의 거리 이다. 이 값을 임의로 두었고, 이를 1로 가정했기에 위 그래프에서 -1, 1 로 그래프를 그린것이다.
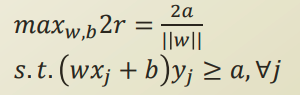
파랑색 위쪽 영역((10, 7) 이라고 가정해보자.) 에서 decision boundary로 점점 값이 낮아진다 라고 생각해보자.
이 값이 파랑색 마지막 평행선에 닿은 순간, 이 값은 a가 된다. 위에서는 1로 가정했으니 1이 될것이다.
강의에서는 한국의 군사분계선으로 예시를 들었다. 법에서 지정한 DMZ라는 영역은 서로 들어가지 못하고, 남과 북에 경계가 있다. 이 경계를 위 SVM의 파랑색, 빨강색 class의 평행선이고, decision boundary의 margin의 영역이 DMZ, DMZ의 정 중앙 평행선(DMZ가 평행하다는 가정.) 이 decision boundary 인것이다.
이 정 중앙의 Decision boundary를 지나는 순간, panalty를 줄 수 있게 된다. 따라서 위 처럼 0부터 loss를 적용할 수 있다.
decision boundary를 지나자마자 1 이라는 panalty를 주는 loss function이 바로 0-1 loss 라고 한다.
하지만 0-1 loss는 quadratic programming에 적용하기 힘든점이 있어서 잘 사용하지 않는다고 한다.
- option 2
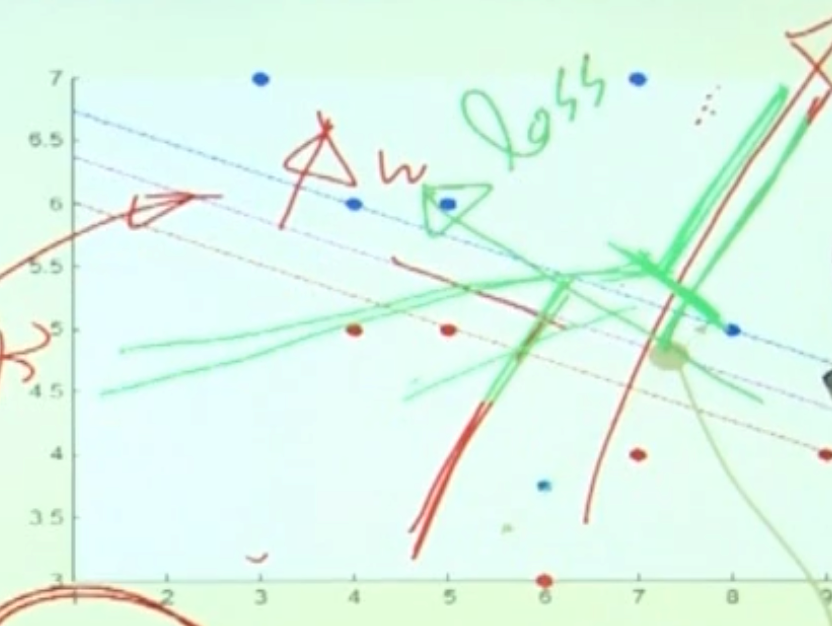
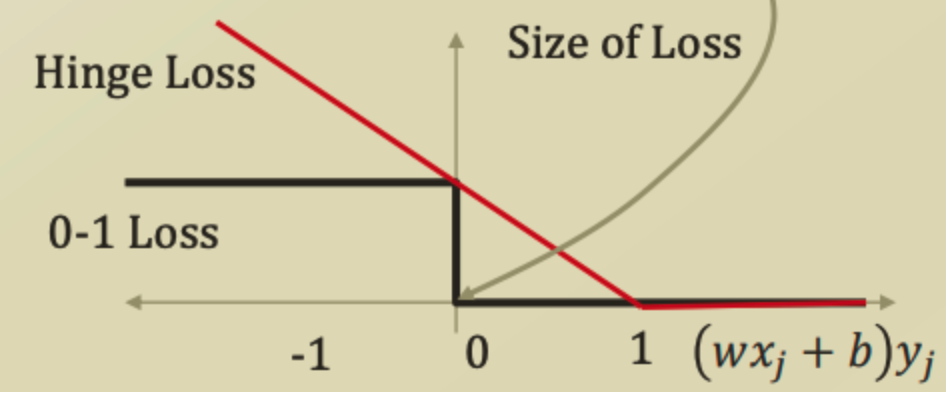
hinge loss는 점진적으로 loss를 주는것이다. class의 경계를 지나서부터 linear하게 loss를 부여한다.

이를 slack variable (여유 변수) 이란것으로 표현한다. C는 loss를 얼마나 강하게 적용할것인지에 대한 parameter 이다.
| 모든 feature에 대한 loss를 | w | 에 더한다. 최종적으로 margin을 최대화 하는 방향으로 학습을 하게 되는것이다. |
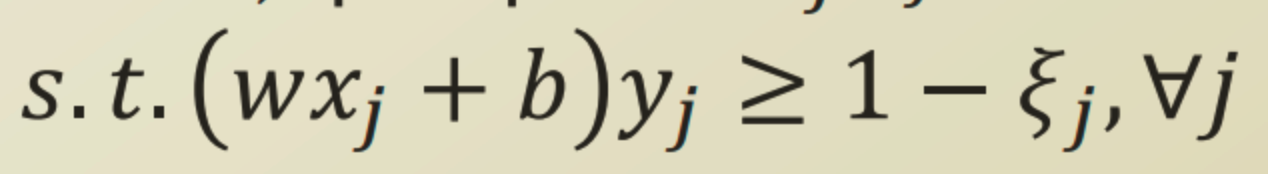
margin을 최대화 하면서, 동시에 slack variable이 0보다 큰 데이터의 수를 최소화하는 W 평면을 찾는것이다.
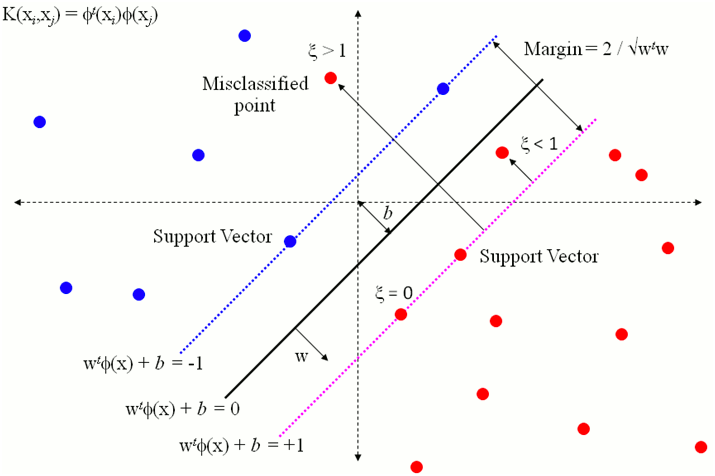
slack variable이 0이라면 올바르게 검증된것이고, 0 < slack variable < a 인 상태면, 오차를 허용하는 상태이고, a 보다 크다면 misclassified 된 상태이다.
출처: