Files: https://strutive07.github.io/assets/images/2_5_How_to_create_a_decision_tree_given_a_training/IE661-Week_2-Part_3-icmoon-ver-1.pdf last update datetime: Jan 04, 2020 5:58 PM

13개의 independent한 value와 1개의 dependent한 value로 이루어진 dataset이 있다고 가정해보자.
우리가 PAC learning(Probably approximately correct learning)
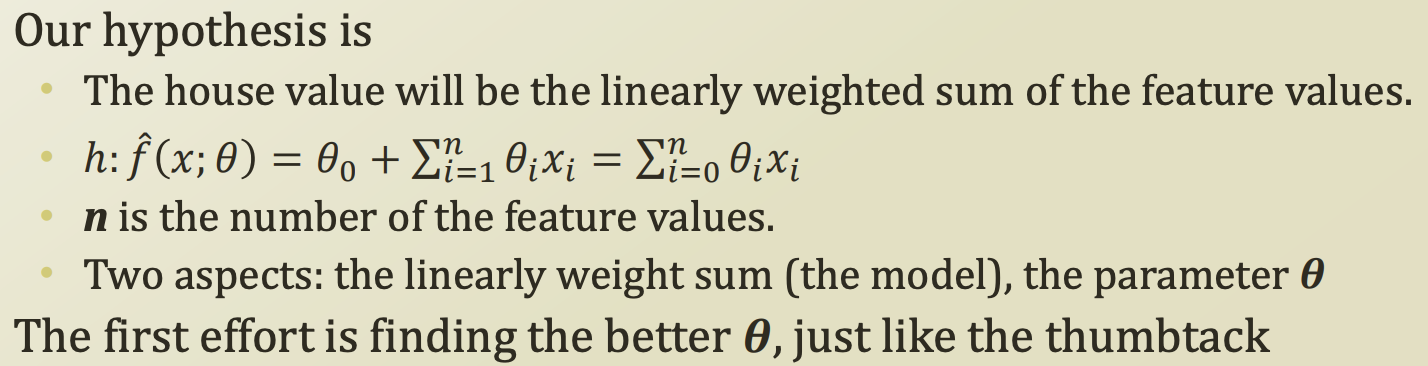
우리의 hypothesis는 house value는 각 feature들을 learnaly weighted sum 한 결과 라고 가정해보자.
theata zero라는 절편을 수식으로 넣어 matrix꼴로 일반화를 하면 다음과 같이 변한다. 절편에 대한 weight를 1이라고 가정하면 합칠 수 있다.
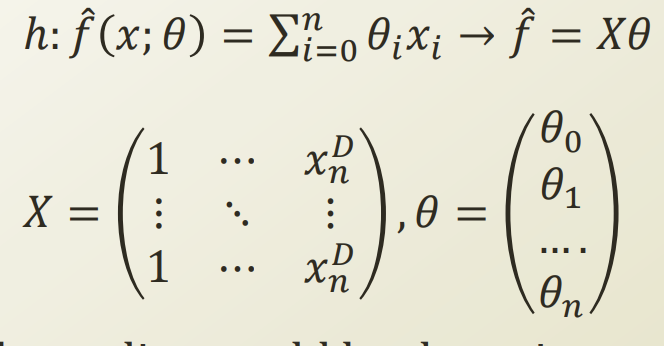
위 hypotheses에 hat이 붙는 이유는, real world에서는 항상 noise가 붙는다. 우리가 가정한 hypotheses에는 noise가 없으므로 가상의 함수이니 hat을 붙여둔것이다.
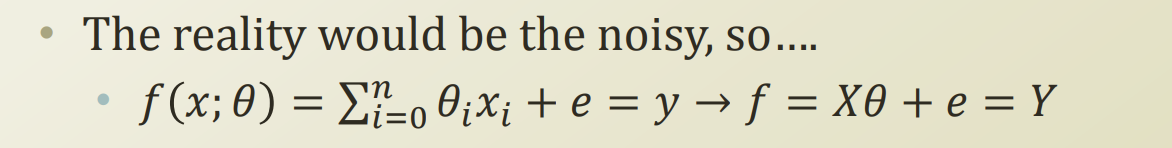
X는 이미 정해져있는것이므로, error를 최소화 하는 theata를 찾으면 우리의 가정이 real world function과 유사해질것이다.
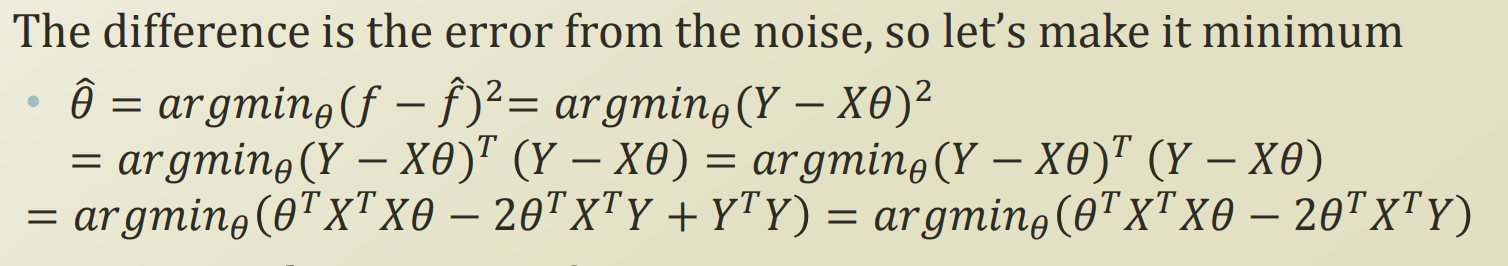
제곱을 준 이유는 다음 강의에서 나온다한다.
matrix 형태이고, 상수 term을 제거하면서 수식을 정리한다.
이번에도 극점을 찾기 위해 theta로 해당 식을 미분해보자.
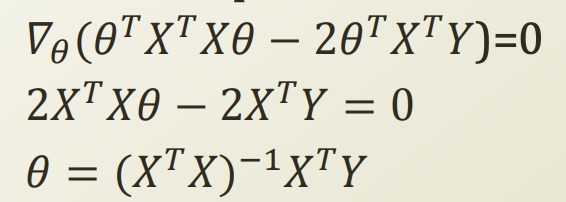
feature가 1개라고 가정하고 그래프를 그려보면 다음과같다.
feauture가 1개일때 절편 theta zero, feature theta one 이 존재한다 따라서 아래와같은 일차 함수가 나오게된다.
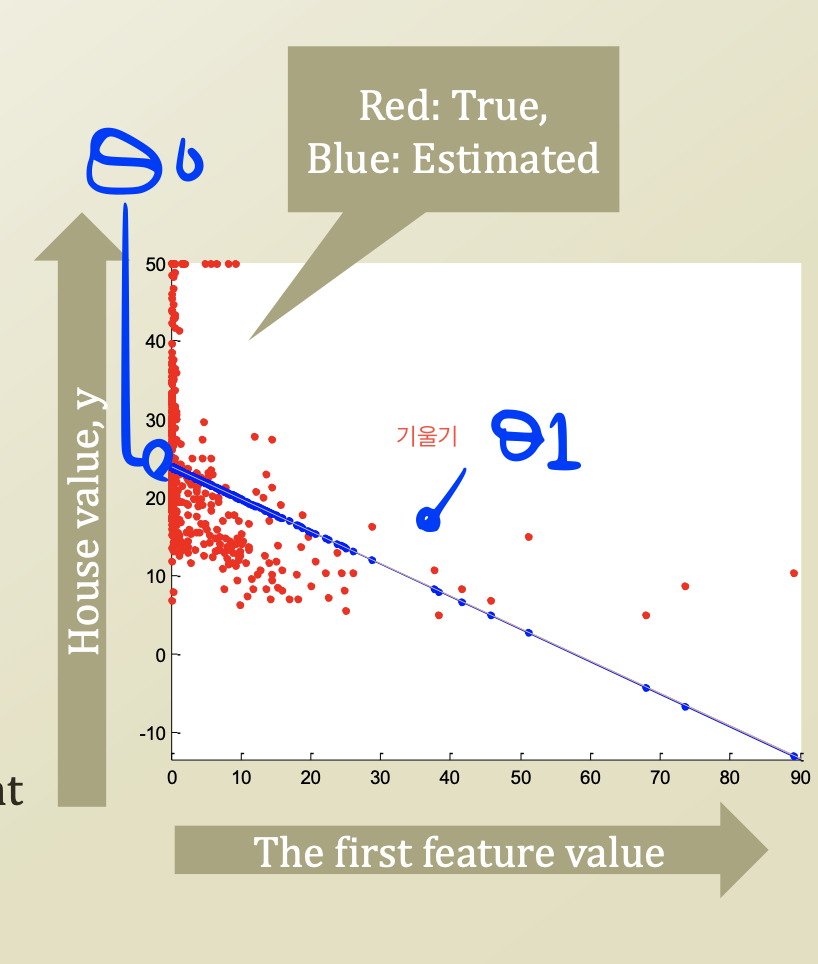
만약에 error가 normal distribution을 따른다면, MLE를 한것과 동일하다.
왜그럴까? 지금 우리가 한것은 통칭 MSE, Mean squared error 인데?

