Files: https://strutive07.github.io/assets/images/2_3_2_4_Introduction_to_Decision_Tree/IE661-Week_2-Part_2-icmoon-ver-1.pdf last update datetime: Jan 05, 2020 10:17 PM
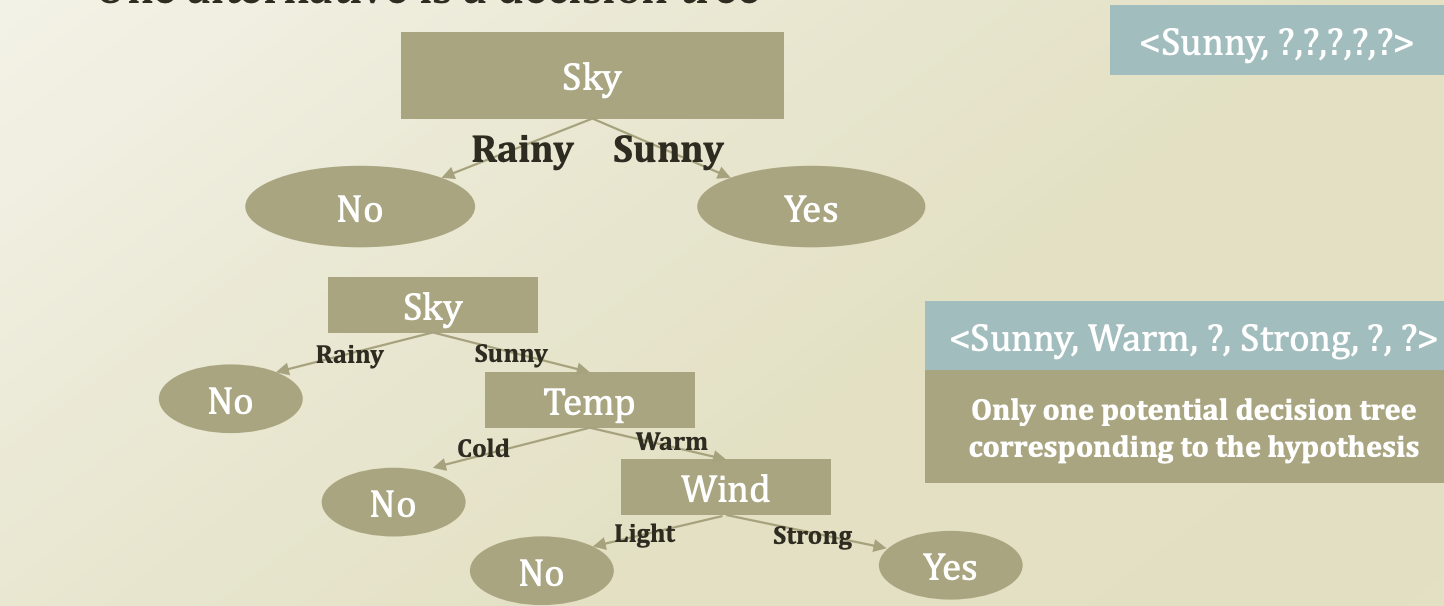
2.2 에서 사용했던 hypotheses를 decesion트리로 나타내면 다음과 같은 형태 이다.
Credit approval dataset
http://archive.ics.uci.edu/ml/datasets/Credit_approval

A1 특성을 사용할 경우, A1이 a일때 무조건 맞다 라고 판단할 경우, b일때 무조건 맞다 일 경우라고 생각해보자.
그럼 위 사진처럼 98 + 206 명은 올바르게, 112 + 262명은 틀리게 판단할것이다.
A9 특성을 사용한다고 가정해보자.
이때는 284 + 23 명은 올바르게 판단하였고, 77 + 206 명은 틀리게 판단하였다.
이처럼 하나의 특성만 사용하면 좋지 못한 결과가 나온다.
Entropy
어떻게 하면 불확실성을 줄일 수 있을까?
예시) 위 decision tree에서 불확실성은, 틀린 수와 비례한다.
불확실성은 측정하는 방식이 바로 entropy이다.
entropy가 높을경우, 불확실성이 높다 라는 의미이다.
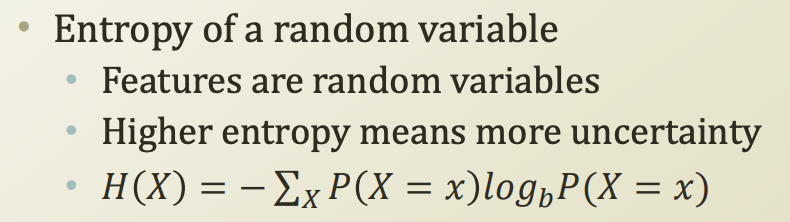
조금 더 정리를 해보자.
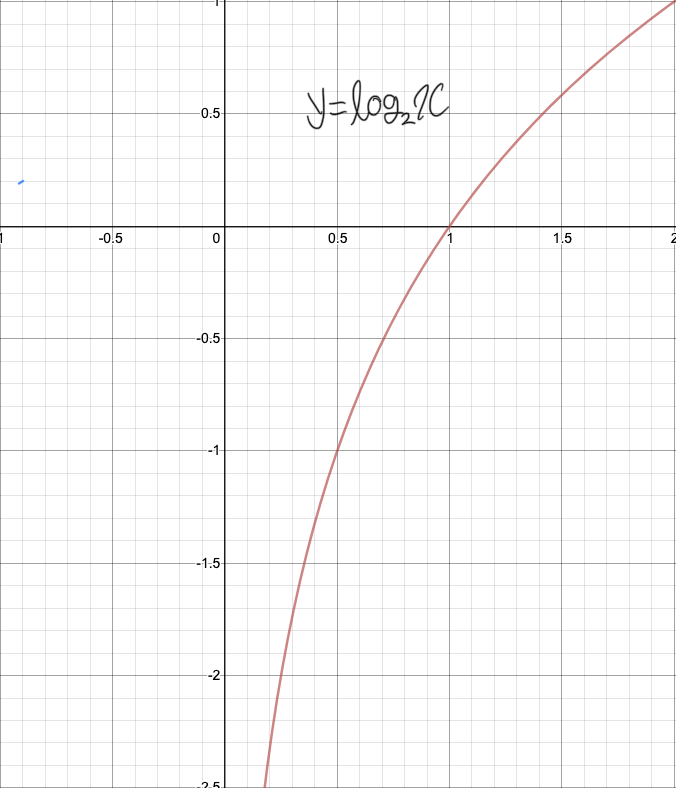
정보량이란?
정보량이란, 위와같이 나타낼 수 있다.
특정 사건에 대한 확률값음 0에서 1 사이이다. 이를 위 함수에 넣으면 결과는 다음과 같이 확률값이 0에 가까울수록 무한대로 발산하고, 1에 가까울 수록 0에 수렴하는것을 알 수 있다.
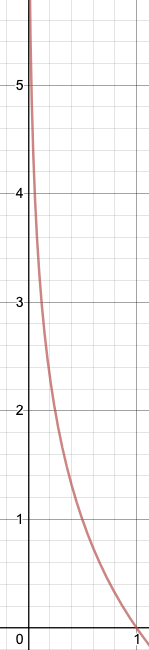
이는, 희소한 확률에 대해 정보량을 더 높게 치는것이다. 마치 알레스카에서 눈이 올 확률과, 아프리카에서 눈이 올 확률에 대한 정보량을 생각하면 좋을듯하다. 희소한 확률을 가지는 사건이 더 많은 정보량을 가지고 있다는것을 의미한다.
엔트로피는, 모든 사건에 대한 정보량을 총합한것이다.
Conditional entropy
X라는 사건이 관측되었을때, Y 사건이 관측될경우의 정보량
간단하게 생각하면된다. Y 사건이 X사건에 dependency가 있는 상태에서, entropy는 모든 사건의 정보량의 총 합을 구해야 한다.
따라서 X 사건 하나당 Y 사건에 해당하는 수많은 정보량들의 합인 엔트로피를 더해줘야한다. 그러니 아래 처럼 Y의 총합을 X에 대해 또 총합을 구해야 하는것이다.
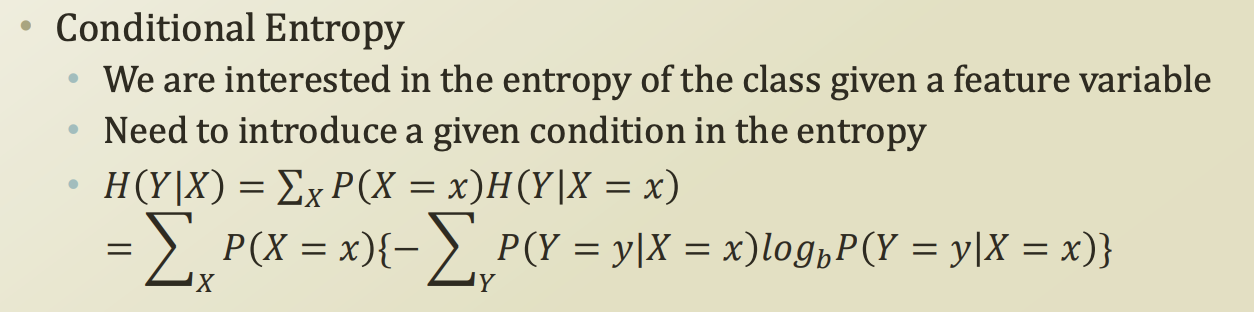
그럼 creadit approval예제에 한번 적용해보자
Information Gain
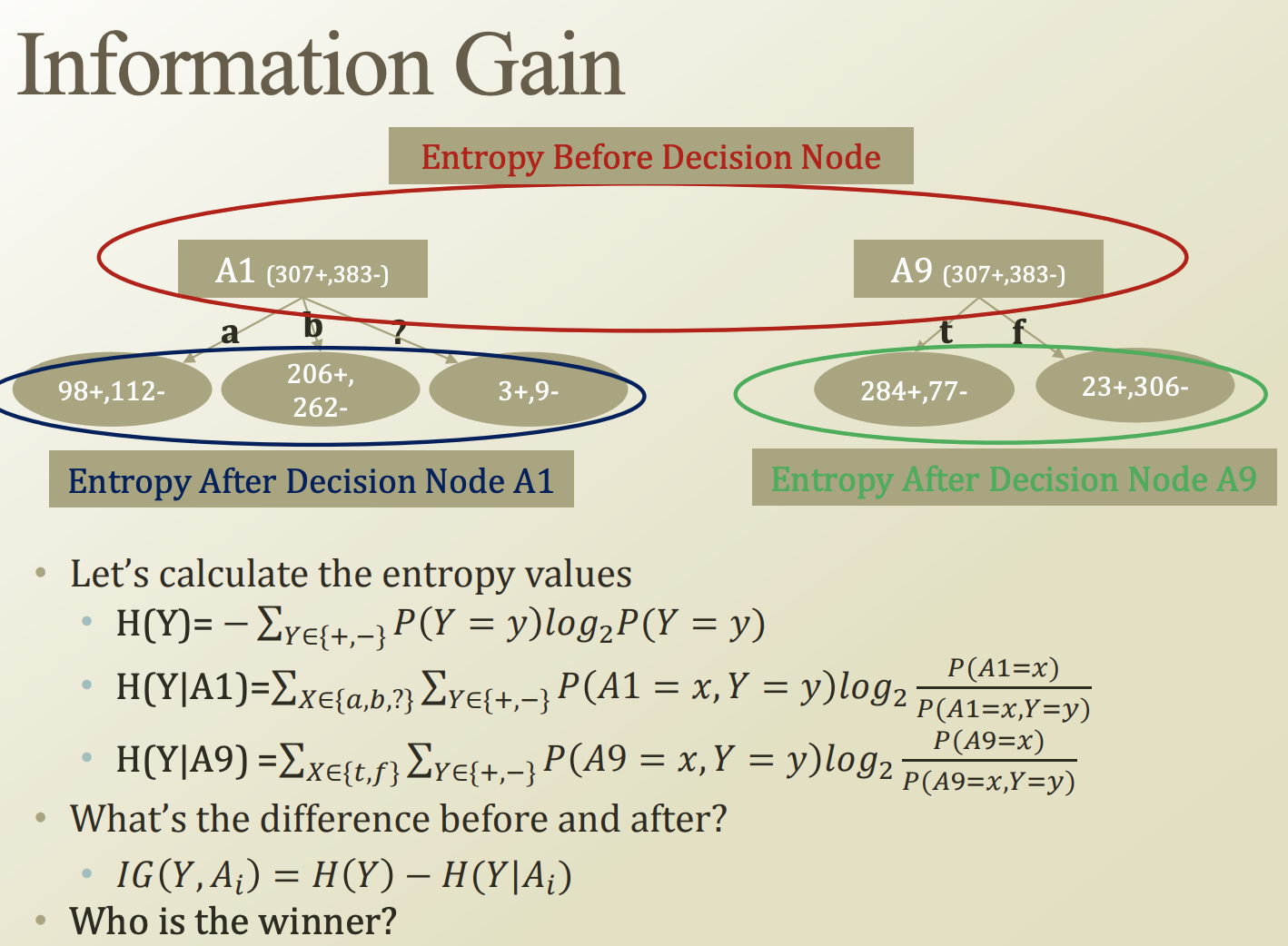
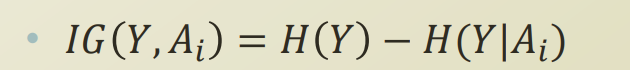
원래 Y는 어느정도 entropy를 가지고 있었는데, A_i를 feature로 선택했을때, entropy가 어떻게 바뀌었다. 그 변화량은 얼마나 되는가? 에 해당하는것이 information gain 이다.
ID3 algorithm
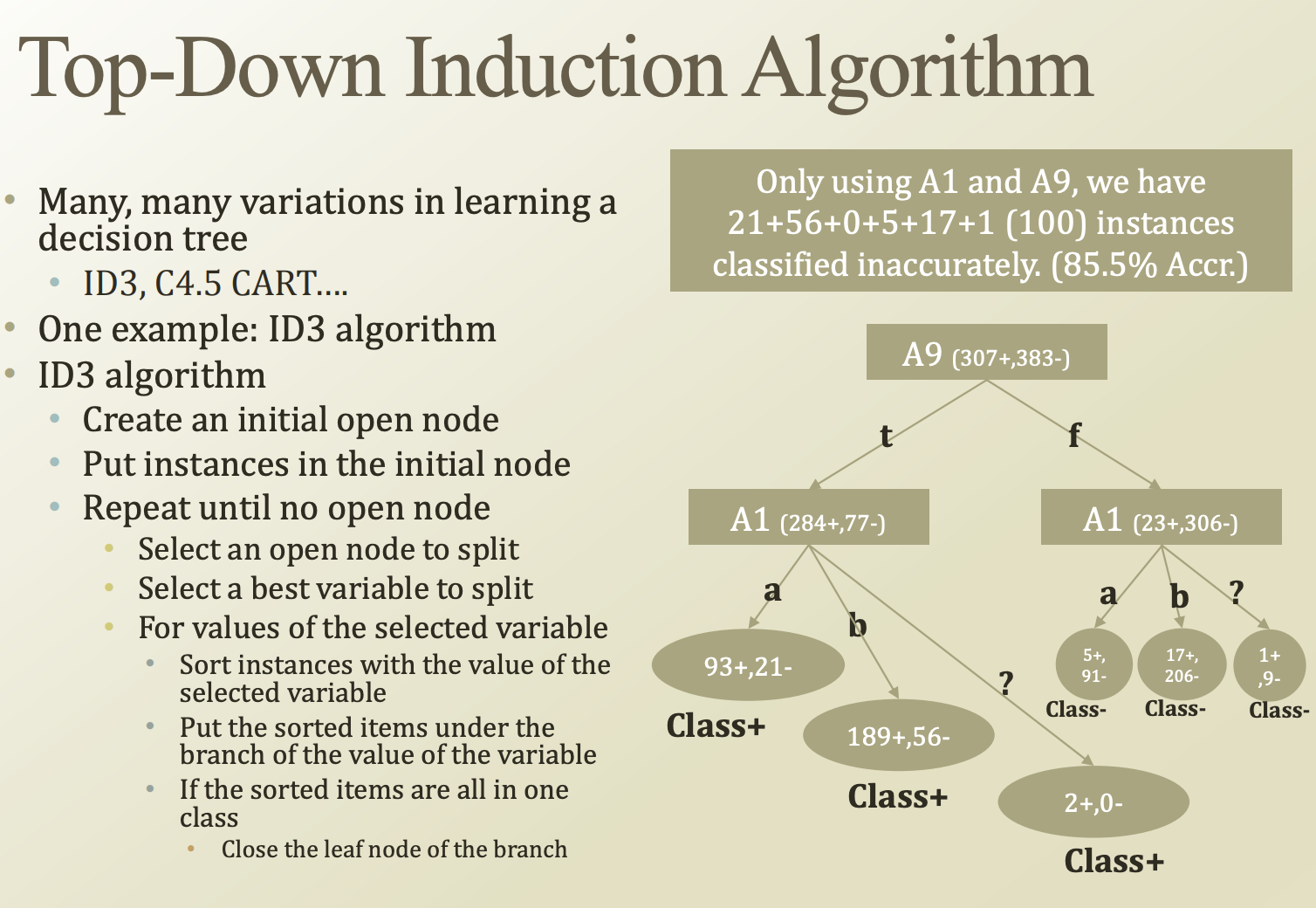
하나의 열려있는 node에서, 각 variable들중 IG가 가장 큰 variable을 기준으로 node를 쪼갠다.
쪼개다 결과가 모두 같은 node가 나올 경우, 그 node를 leaf node로 하고 해당 node를 닫는다. 더이상 쪼개지 않는다.
모든 노드가 닫힐때까지 반복한다.
예시) https://bskyvision.com/598
Problem of decision tree
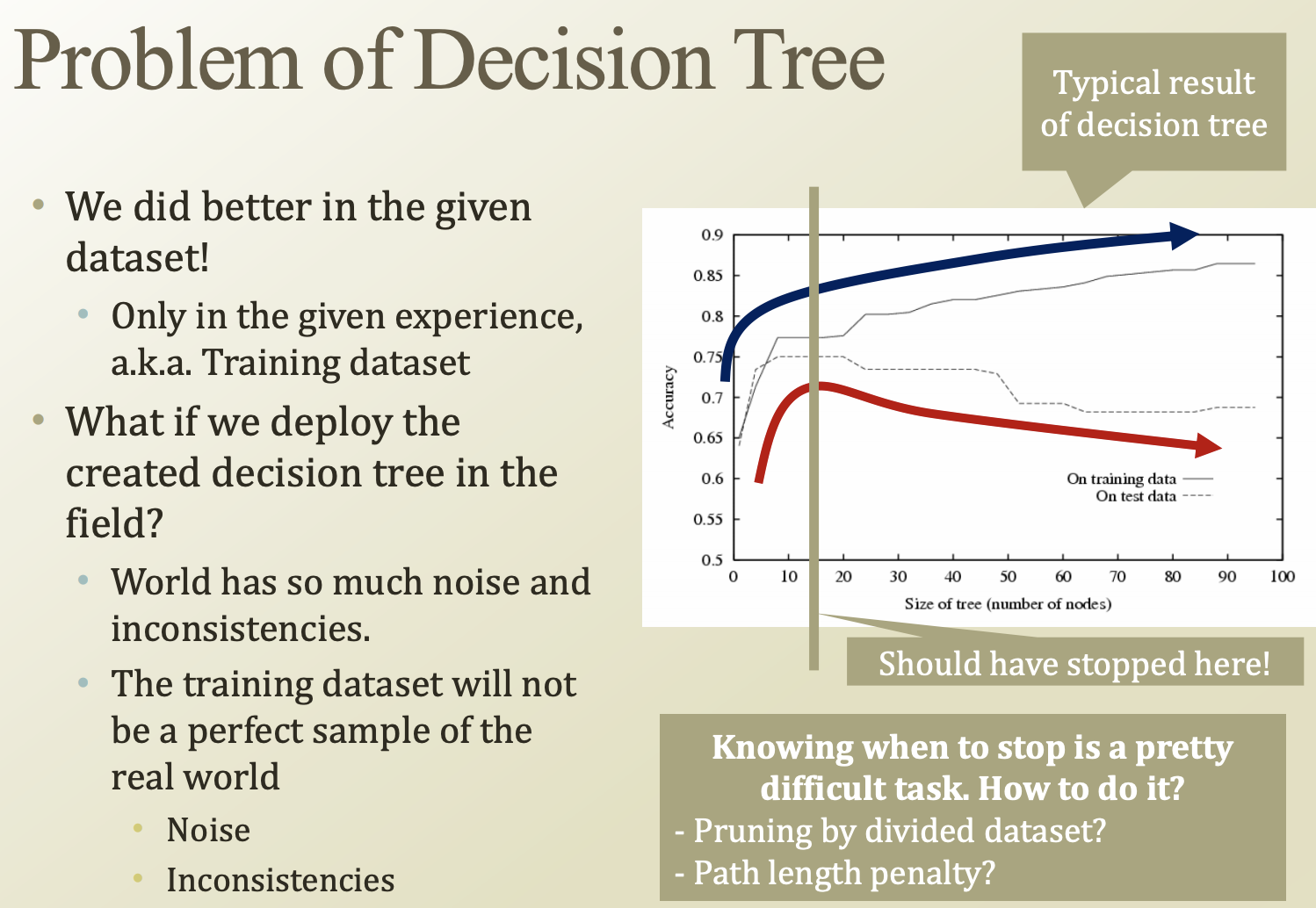
decision tree의 문제점은, training dataset에 overfitting된다는점이다.
조금만 데이터가 변해도 tree의 모양이 급격하게 변할 수 있고, 해당 데이터에 noise와 inconsistencies들이 많으면 test시의 tree의 정확도는 계속 떨어지게된다.
Rule base machine는 쉽게 구현할 수 있고, interpretable하다.
하지만 perfect world가 아닌 경우, dataset에는 필연적으로 noise가 있다. 따라서 정답에 수렴할 수 없는 경우가 필연적으로 존재한다.