last update datetime: Feb 06, 2020 1:34 AM
Optimization problem
일단 최적화 이론부터 잠시 살펴보자.

출처: https://wikidocs.net/17203
Mathematical optimization problem은. 최적화 해야할 variable이 있고, objecctive function f가 있는 상태에서, inequality constraint function, equality constraint function 등이 존재하는 경우 이다. 이 제약조건을 만족하는 경우에서 objective function f 를 최소로 만드는 x’ 를 찾는것이다.
Convex Optimization problem
위 inequality constraint function이 convex function 이고, equality constraint function이 affine function인 경우에 convex optimization problem 이라고 할 수 있다.
Convex set
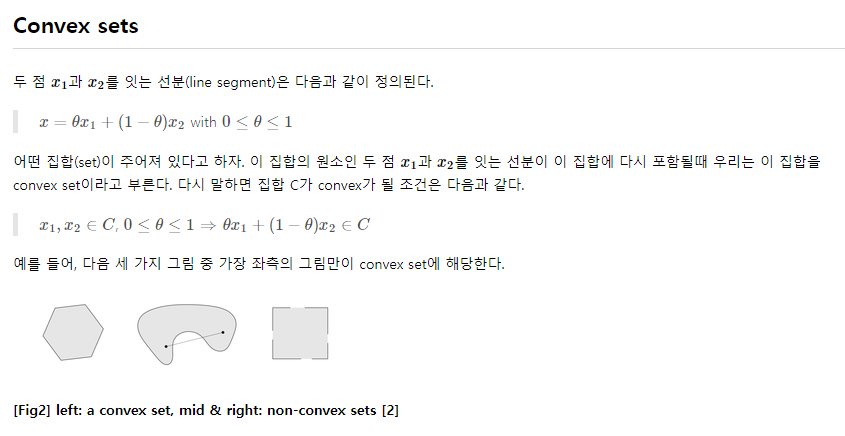
결국 Set 이 오목한 구간이 없고, 볼록하기만 해야한다. 그걸 위 수식으로 나타낼 수 있다.
Convex function
convex funcion 또한 동일하다. domain이 convex set에 있어야 하므로 볼록 함수가 되야한다.

Convex function은 볼록함수이기 때문에, local minimum이 항상 global minimum 이다.
Canonical problems
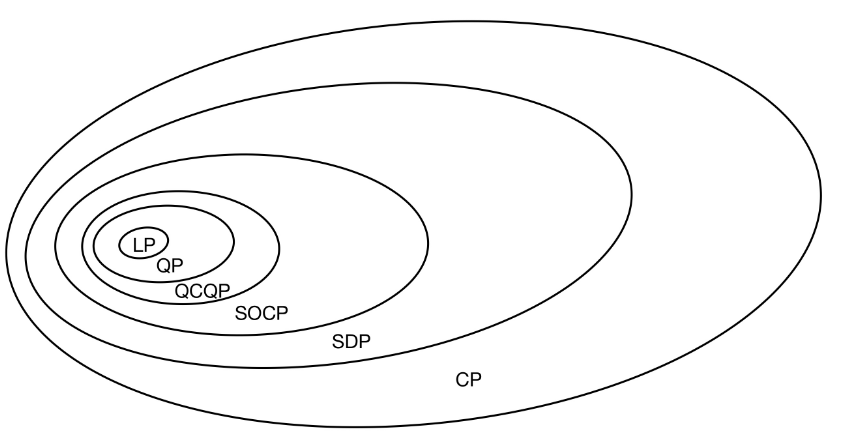
convex optimization problem에서 object function 과 constraint function의 유형에 따라 optimization problem을 다양한 범주로 나누고, 위와 같은 포함 관계를 가진다.
여기서 Linear programming과 quadratic programming을 알아보자.
Linear programming
General LP
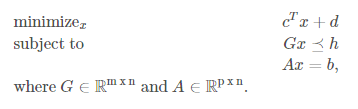
objective function과 constraint function이 모두 affine function일 경우, 이 문제를 linear program 이라고 부른다.
이 문제는 기하학적으로, polyhedron 형태의 fessible set에 대해, affine function(c^Tx + d)을 최소화 시키는 x’ 으로도 해석된다.
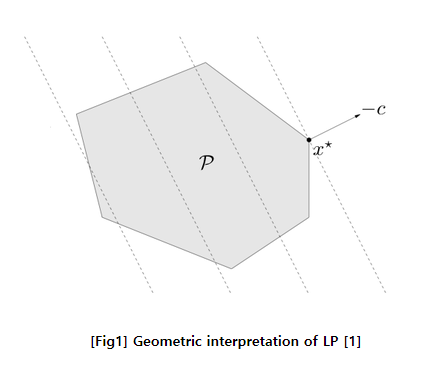
General form 보다 조금 더 scope 이 작은 standard form도 존재한다.
Standard form
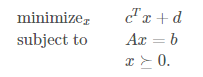
constraint 를 equation 만 가능하게하고, target variable은 non-negative variable 만 가능하도록 제한한다.
또한, 모든 general LP 는 다음 과정으로 standard LP 로 변형시킬 수 있다고 한다.
Convert general form to standard form
-
slack variable을 사용하여 inequality constraint 를 equality constraint 로 변환
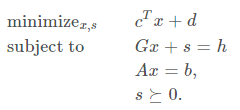
-
variable x 를 두 개의 non-negative variable로 치환. x=(x^+) − (x^−)이고, (x^+), (x^−) ⪰0.
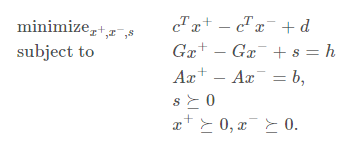
-
아래 행렬 정의
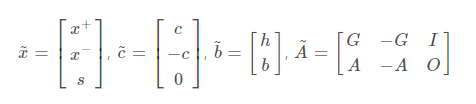
-
수식을 위 행렬로 변환
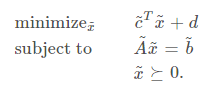
Quadratic programming
quadratic programming 은 objective function이 이차식(convex quadratic)이고, constraint function이 모두 affine funtion인 convex optimization problem 이다.
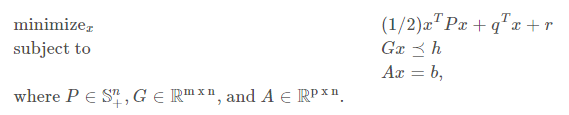
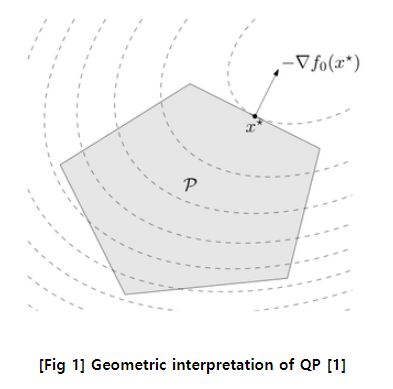
linear programming 때와 비슷하게, 기하학적 polyhedron 형태의 fesible set 에서 objective function을 최소화 시키는 x’ 을 찾는것으로 해석된다.
linear program 때는 affine 변환에 사용되는 방향을 수선의 방향으로 설정해서 찾았다면, Qp 에서는 x’ 에서의 미분값의 수직 방향으로 하는듯하다.
Reference
https://www.youtube.com/watch?v=GZb9647X8sg