Create time: Feb 06, 2020 11:47 PM Update time: Feb 07, 2020 8:37 PM
머신러닝을 하면서 최적화 이론에 대해 하나도 모르고있었다.
Convex optimization의 정말 유명한 강의인 stanford EE364A 를 빠르게 수강해볼 예정이다.

1강은 mathematical optimization, linear programming, convex optimization 등에 대해 배우고 예제를 살펴본 후 non-linear optimizaiton 등을 배워볼 예정이다.
Mathmetical optimization

f0(x) 라는 특정 objective function 이 있다. 여기서 최적화 해야하는 변수 x 가 있고, 이는 n 차원의 vector 라고 가정해보자.
f_i(x) 는 constraint function이고, 일단 여기서 inequality funciton 이라고 하자.
상수 b_i 는 constrant의 limit, bound, budget 이라고 생각하면된다.
x vector의 모든 element가 위 constrant function을 만족하면서, objective function을 최소화하는 x를 x’ 이라 하자. 이 x’을 찾는것이 mathematical optimization problem 이다.
Example

예시를 하나 살펴보자.
portfolio optimization이 있다고 해보자.
특정 주식 포트폴리오를 만들것이고, varible 로는 여러 주식들이 있을것이다.
제약 사항으로는 예산이 있을것이고, 수익률등도 제한할 수 있다.
objective function은 risk, return variance 등을 설정할 수 있다.
이를 data fitting, machine learning 입장에서 생각해보자.
variable은 우리가 만들어나갈 model의 parameter들이고,
제약사항은 prior, parameter limit 들이 있을것이다.
objective function은 loss function이 될것이다.
베이지안 framework 에서는 negative log posterior probability가 될것이고, SVM 에서는 hinge loss, zero-one loss 등이 있을것이다.
또한 log likelihood 등도 있다. 이것들이 implausibility에 대한 지표를 funciton으로 나타낸것이다.
MAP 등의 방법으로 이를 minimize 하면 될것이다. 수많은 방법이 있을것이다.
Solving optimization problems
사실 현실에서는 풀기 엄청나게 힘들다. 대부분 NP Hard 할것이다.
수천년에 걸쳐서 찾은 minimum은 global minimum 이다. 이를 구하기는 너무 힘드니, 똑똑하신 분들이 근사하여 찾아낸 일종의 답 같은것을 구한다.
여기서 일부 효율적으로 최적화를 할 수 있는 방식들이 있고, 아래 방법들이 그 예시들이다.
- least-squares problems
- linear programming problems
- convex optimization problems
Least-squares problems
least-squares problem은 AX-b의 유클리디언 norm을 최소화하는 X 를 찾는것이다.
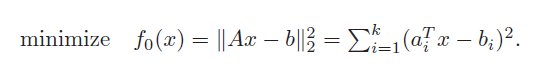

analytical 하게 구하면 아래 처럼 구할 수 있을것이다.
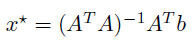
또한, 시간복잡도는 다음과같다.
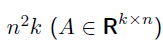
여기서 n 은 norm 의 차원(유클리디언이니, 2) k 는 row 개수 이다.
이 기술은 굉장히 성숙한 기술이다. 내부적으로 어떻게 돌아가는지 몰라도 될 정도로.
물론 A 가 sparse 해서 어떻게 어떻게 해서 시간복잡도를 줄일수도 있을것이다. 하지만 대부분의 경우에서는 이미 구현되어있는 알고리즘들은 믿고 사용할 만큼 효율적이다. 힘들여서 구현하지 말라는 소리인듯도 하다..(모든 사람이 이 black box를 알 필요도 없다 라는 뜻인듯하다.)
해당 문제가 least-squares problem임을 알아차리는것은 굉장히 간단하다. objective function이 quadratic function인지만 확인하면 된다. 그리고 위 공식을 사용하면 끝난다.
여기서 실제로 적용하기 위해 몇가지 테크닉들이 있다.
-
weighted least-squares
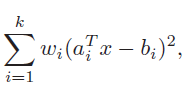
W_i 는 positive 이다. 각 i 에 대해 Ax - b에 가중치를 줘서 다르게 대하겠다는 것이다. 이 방식은 linear measurments 들이 unsequal variances error 로 오염되었을때 사용한다 한다.
-
regularization
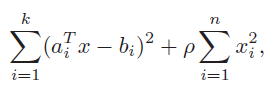
regularization은 cost function에 추가적으로 term 을 추가하는것이다. 페널티를 추가하는것이다.
이 방식은 보통 예측해야하는 x 가 prior disbribution 일 경우 많이 사용한다고 한다.
Linear programming
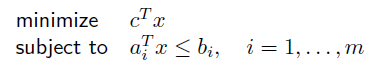
objective funciton과 constraint function이 모두 linear function인 경우 linear programming 이라고 한다.
linear programming 에는 analytical solution이 없다고 한다.
시간복잡도는 least-squares problem 과 동일하다.
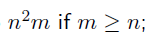
Convex optimization problem
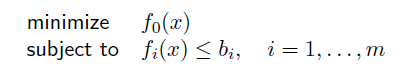
objective funciton 과 constraint 모두 convex function 이여야 한다.
convex optimization problem도 analytic al solution이 없다고 한다.

시간복잡도는 위와 같음. 미분을 해야해서 미분 시간이 포함된다고함.
Example

위와같은 lamp 가 있다고 해보자. lamp 의 파워는 p_max 까지 낼 수 있다고 해보자. 제한된 램프 power로 원하는 조명을 얻어보자.

least - squares 방법을 사용할 수 있을것이다. 왜냐? objective function이 quadratic이므로.
weighted least-squares 방법도 사용할 수 있다.
또한 objective function과 constraint function 모두 linear function 형태로 나타낼 수 있다. 따라서 linear programming으로도 풀 수 있다.
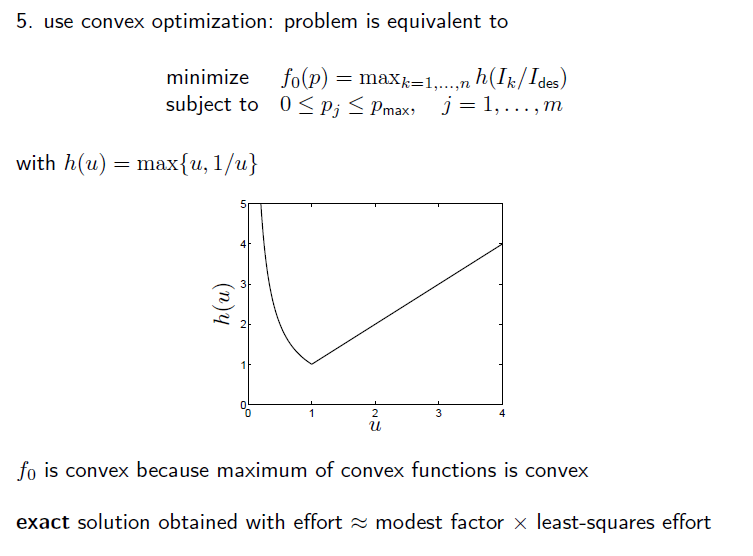
위와같이 objective function을 convex function 으로 만든다면, convex optimization도 사용할 수 있다.
