Create time: Feb 06, 2020 11:47 PM Update time: Feb 08, 2020 2:39 AM

Affine set

x1 와 x2 라는 점 이 있고, 모든 set 이 이 두 점을 이은 선 위에 있을경우, affine set 이라고 한다.

이를 다음 수식으로 표현 할 수 있다.

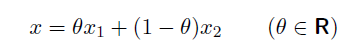
Convex set

line segment 란, 두 점을 잇는 선중 left 끝과 right 끝이 각 점인 선 이다. 다음과 같은 그림으로 그려질 수 있다.

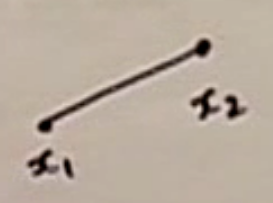
이는 아래 수식에서, theta가 0 ≤ theta ≤ 1 이면 된다.

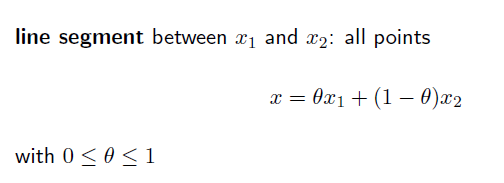
Convex set 이란, 특정 집합에서 두 점을 뽑았을때, line segment 가 모두 그 집합에 항상 포함된다면 Convex set 이라고 할 수 있다.

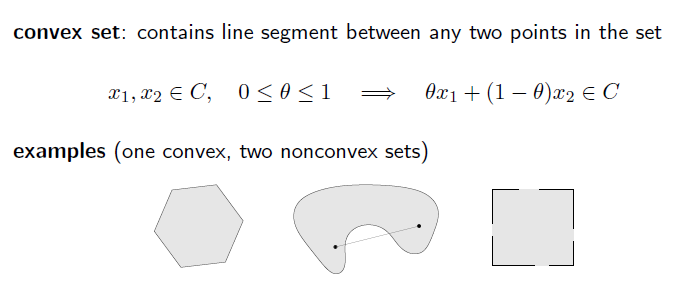
맨 왼쪽은 linear segment가 모두 set에 포함되므로 convex set 이고

중간은 일부가 포함이 안되므로 convex set 이 아니다

오른쪽은 가장자리가 일부 포함이 안되어있으므로 convex set이 아니다.

Convex combination and convex hull

Convex combination이란, convex set에 있는 k 개의 점들을 theta로 wegith sum을 한 값이다. 이때 weight들의 합은 1이여야 하고, 모두 0보다 커야한다.

이를 기하학적으로 살펴보자.

아래 세 점이 convex set에 포함된다고 하자.

이때 convex combination의 set 은 다음과같은 모양을 가진다.

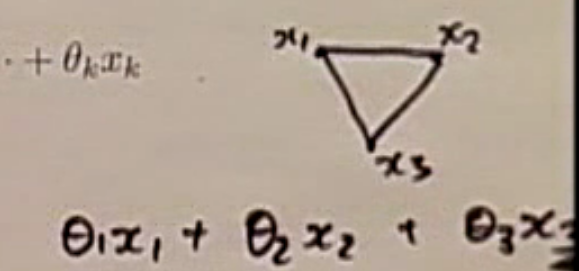
Convex hull 이란, convex combination을 모두 포함하는 가장 작은 단위 이다.

Convex cone

Cone은 하나의 방향으로 무한히 진행되는 집합이다. 또한 원점을 포함해야한다.

Convex cone은, 집합이 cone 이면서 convex 해야한다.

위 그림처럼 원점에서부터 두 점을 경계로 퍼져나가는 집합이다.

Hyperplanes and halfspaces

hyperplane은 선형 방정식으로 만들어질 수 있는 특정 평면이다.

이게 1차일경우 선, 2차일경우 평면 등이 된다.

b가 0인경우 원점을 지나간다.

halfspace는 는 hyperplane을 기준으로 양쪽으로 나뉘어지는 공간을 말한다.

hyperplane은 선형 방정식이므로 affine 하고 convex 하다. 또한 halfspace 공간이므로 affine하지는 않고, convex 하다.

Euclidean balls and ellipsoids

Euclidean ball은 수학적으로 원을 뜻한다. Euclidean norm이 2차원을 의미하므로, 이는 중심에서부터의 거리가 r 보다 작거나 같은 공간을 뜻한다.

Euclidean ball 또한 convex set 이다.

이에대한 증명은 다음과 같다.

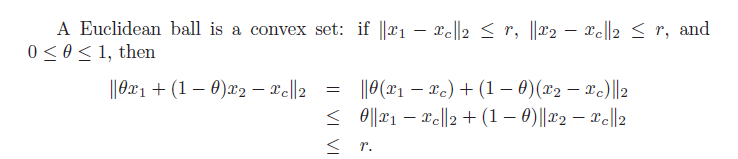
ellipsoid(타원면)은 다음과같이 정의된다.

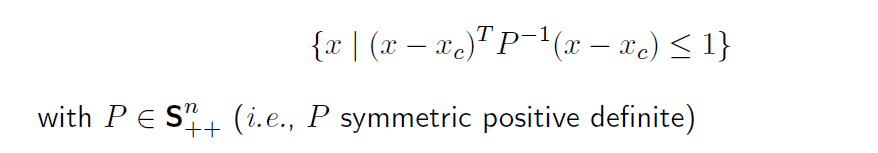
P 는 대칭에 positive definite이므로 아래 수식을 만족해야함.

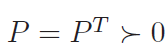
행렬 P 는 ellipsoid 가 중심 x_c에서 모든 방향으로 얼마나 멀어지는가를 나타낸다. 타원의 모양을 나타내는것.

Norm balls and norm cones

위의 타원은 유클리디언 norm 이였다

Norm은 다음과같이 정의할 수 있다.

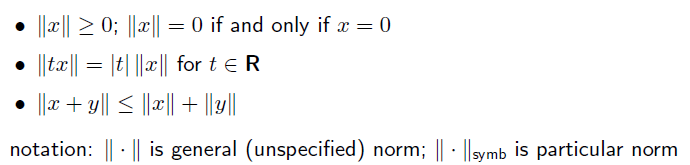
유클리디언에서 했던것 처럼, 특정 범위 내의 norm을 norm ball이라고 하고 살펴보면 다음과 같은 그림이 될것이다.

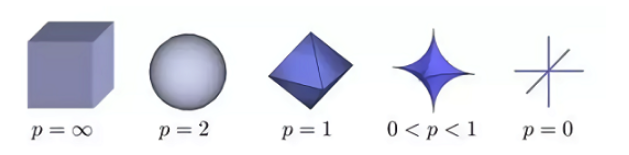
2D 로 살펴보면 다음과같으 모양이 된다.

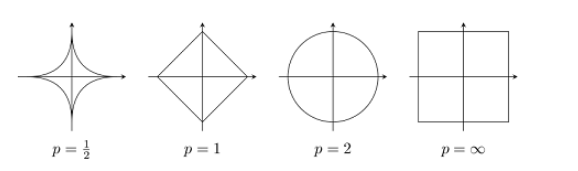
Norm cone 반경이 norm 으로 정의된 cone 이다. 아래 는 원 모양의 유클리디언으로 생성된 유클리디언 cone 이다. cone 은 원점에서 빛을 쐇을때를 생각하면 된다.

norm 은 n=1 이상일 경우 cn

Polyhedra

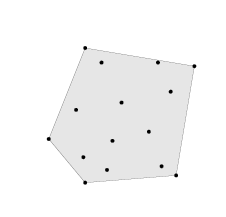
polyhedron은 선형 부등식과 선형 등식의 교집합으로 정의된다.

위 그림은 5개의 halfspace의 교집합으로 이루어진 polyhedra 이다.

polyhedra 또한 convex 하다.

Positive semidefinite cone

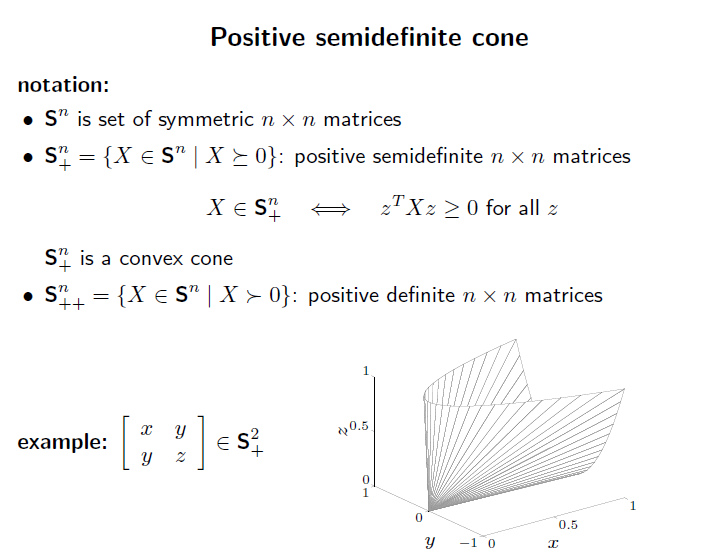
positive semi definite cone 은 positive semi-definite 을 사용하여 cone 을 구성한것이다.

위에처럼 2차원 예제라면, 특정 matrix가 나타내는 공간이 있고, 이를 0,0에서 빛을 쏴 cone을 구성한 것이다.

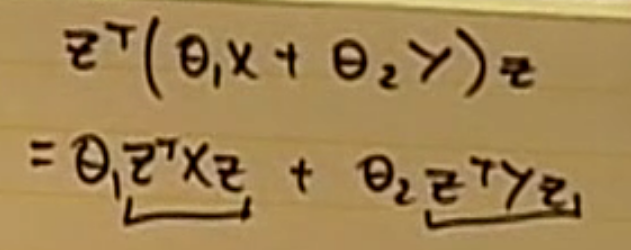
positive semi-definite 끼리 cone을 구성한 것이므로, 그 결과도 positive-semi-definite 하므로 convex set 이다.

Operation that preserve convexity

특정 집합이 convex set임을 판별하기 위해서는 우리가 앞에서 배웠던 definition을 적용하는 방법이 가장 정도일 것이다.

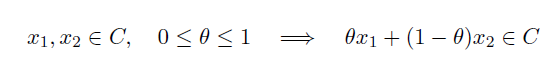
여러 연산을 거칠 경우, convex set 의 convexity를 유지할 수 없는 상황이 올 수 있다. 이럴때는 아래 연산들을 통해서 convexity를 유지하는 방법을 알아보자.

intersection

convex set 의 교집합은 convex set 이다.

Affine function

affine function에 대한 수학적 정의는 다음과같다.

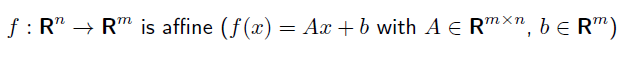
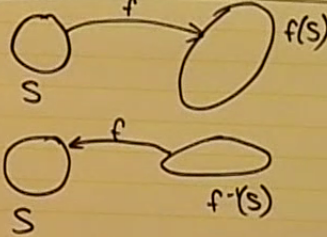
원본이 convex set 이였다면, affine function을 거쳐도 convex set 이다.

이는 역도 성립한다.

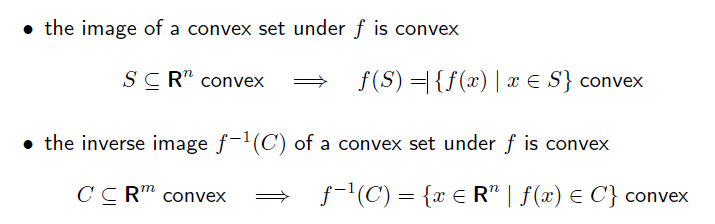
이 예로 scaling, translation, projection등을 거쳐도 원본 set 이 convex set 이면, 결과도 convex set 이다.

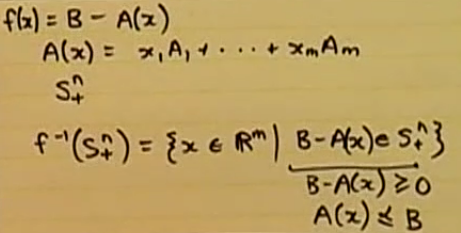
Linear matrix inequality의 해집합 또한 convex set 이다.

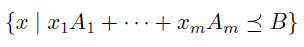
Perspective function and linear-fractional function

perspective function은 사람이 눈에 보는듯 물체를 변형시키는것이다. 가까이있는것을 크게, 멀리있는것을 작게.

perspective 이 convex 할 경우, image 와 inverse image 또한 convex 하다.

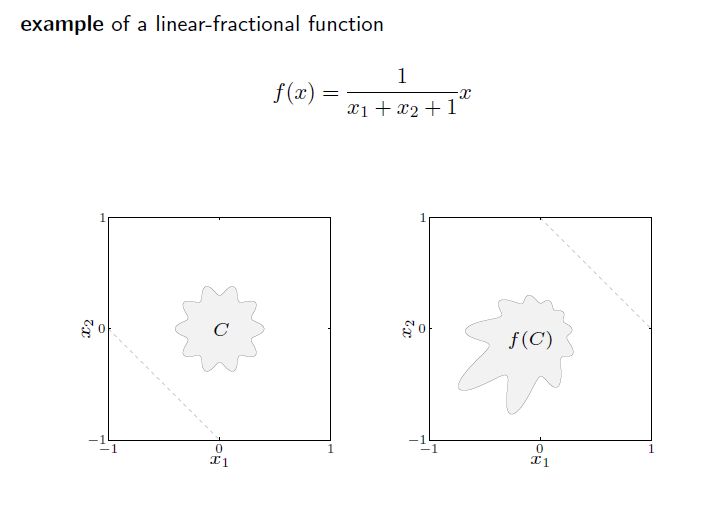
linear - fractional function은 perspective function 과 affine function으로 구성된다.

두 함수 모두, 정의역이 convex set 일 경우, image 와 inverse image 모두 convex set 이 된다.

Generalized inequalities

실수 공간에서 Convex cone 이 proper cone 이려면, 다음 성질을 만족해야한다.

• K is closed - boundary 를 포함한다
• K is solid - interior 가 emtpy가 아니다. 고 차원에서 저차원 cone 을 설정할 경우.
• K is pointed - 직선을 포함하지 않는다. negative 방향에서 cone 이 닫혀있지 않은 경우.

proper cone

not proper cone

사실 이건 convex cone 도 아니다.

generalized inequalities는, N 차원 공간에서 좌표 끼리 inequality 를 측정하는 방법이다.

proper cone 을 사용하면 generalized inequality를 정의할 수 있다.

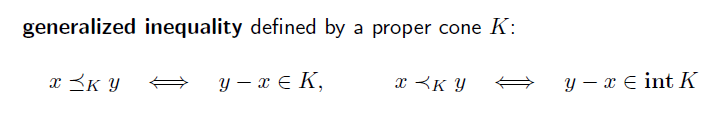
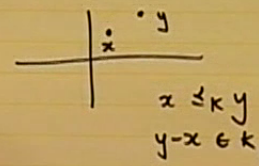
y-x 가 우리가 정의한 cone 내부에 있다면, x 는 y 보다 작은것이 될 것이다.

Minimum and minimal element

이제 generalized inequality 에서 minimum 과 maximum을 정의해보자.

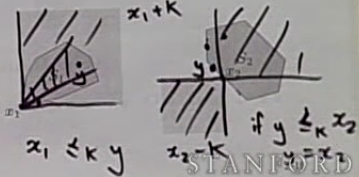
Minimum element

proper cone 에 있는 모든 element 들이 x 보다 generalized inequality 비교를 해서 클 경우, 이를 minimum element 라고 한다.

따라서, minimum element는 무조건 하나 존재한다.

Minimal element

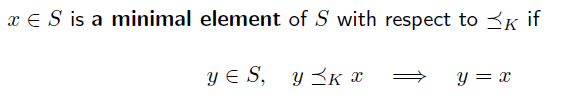
minimal element는 여러개 존재할 수 있다. proper cone K 가 있고, x - k 와 집합 S 의 교집합이 x 하나 뿐이고, y ≤_k x 인 경우가 y = x 인 경우 뿐 이라면, x는 집합 s 의 minimal element 이다.

Separating hyperplane theorem

두 disjoint 한 convex set 은, 그 두 disjoint set 을 나누는 hyperplane이 존재한다.

Supporting hyperplane theorm

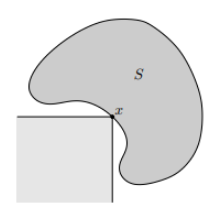
Nonempty set C 에서, boundary 가 하나 있고, 이 boundary가 set C 에 하나의 점 x0 을 공유하고 있으면서 아래 조건을 만족할 경우, support hyperplane 이라고 한다.

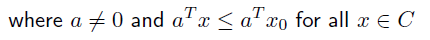
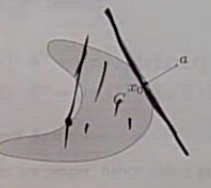
기하학적으로 보면, support hyperplane은 점 x0 에서의 set C 의 접선으로, 공간에서 set C 를 분리하며 이 점을 기준으로한 halfspace 는 set C 를 포함한다.

또한 convex set 일 경우, boundary에서 supporting hyperplane을 찾기 매우 쉽다. 아래 그림 참조.

Dual cones and generalizaed inequalities

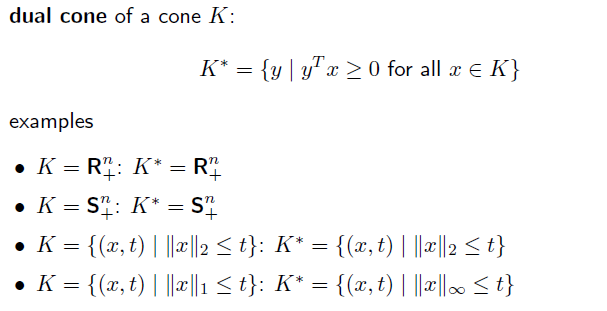
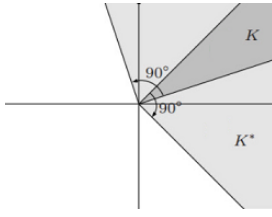
dual cone 이란, set 의 점과 내적했을때 0보다 큰 점인 y 의 집합이다.

기하학적으로는 아래와같이 90도 기울어진 모든 영역을 나타낸다.

dual cone은 원본의 cone이 convex 가 아니여도, 무조건 convex cone 이다.

Minimum and minimal elements via dual inequalities

Minimum element

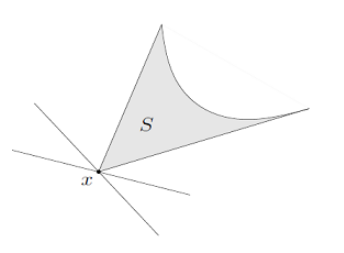
x 가 lambda^T z 의 unique minimizer 라면, generalized inequality에 대해 x 는 S 의 minimum element이다.

기하학적으로 보면, x 는 S 의 strict supporting hyperplane 이다. (점 x 에서만 hyperplane이 교차함.)

Minimal element

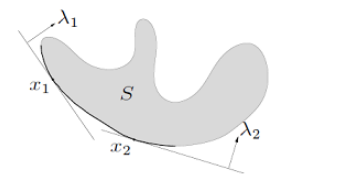
minimal elelemt 의 경우, 필요 조건과 충분 조건 사이에 차이가 있다.

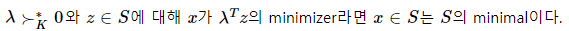
이때 x 는 unique minizier 가 아니다. 위 람다 1 을 보면, 볼드 처리된 영역이 람다1의 minimizer 인 영역이다.

하지만 반대는 성립하지 않는다. 점 x 가 집합 S 에 minimal 하더라도, 특점 lambda 와 내적을 진행한 결과 그 람다의 minimizer가 아닐 경우도 있다.

아래 그림은 set S 의 minimal 이지만, 람다 에 대한 minimizer 가 아닌 경우이다.

Optimal production frontier

이해불가.

그냥 특정 lambda 에 대해, minimal 을 찾는것을 경제학 용어로 풀어쓴다는 느낌밖에 들지 않는다.