Create time: Feb 06, 2020 11:47 PM Update time: Feb 09, 2020 11:05 PM

Definition of Convex function

domain이 convex set 이여야 한다.
그리고 convex function 에서 두 점을 뽑아서 line segment 를 구성했을때, function 의 값은 해당 line segment 보다 작거나 같아야한다. 즉, 볼록함수여야함.
무조건 bolw shape 일 필요는 없지만 positive curvature이여야 한다.

위 식에서 equality를 제거하면, strictly convex functinon이 된다.

Example on R

affine function은 위 수식에서 line segment == funciton 인 상태이다. 직선
사실 R 공간 안에서는 함수를 2차원적으로 그릴 수 있다. 그래서 강의에서는 그저 함수를 그려보고, 커브가 어떻게 형성되는지 보는것으로도 어느정도 convex function인지 알 수 있을것이라 한다.
Examples on R^n and R^{m×n}

vector 공간에서 affine function은 convex 하다. 또한 p≥1 인 모든 norm 또한 convex 하다. 이는 2강에서 배웠던 내용. matrix 공간에서도 convex 하다.
tr 는 선형대수학에서 matrix의 대각합을 뜻함. 행렬의 곱에 대각합을 적용하면 다음과같이 연산된다.

Restriction of a convex function to a line
해당 내용에 대해 좋은 QnA가 있어서 가져옴.
What does it mean to restricting a function to a line in convex optimization?
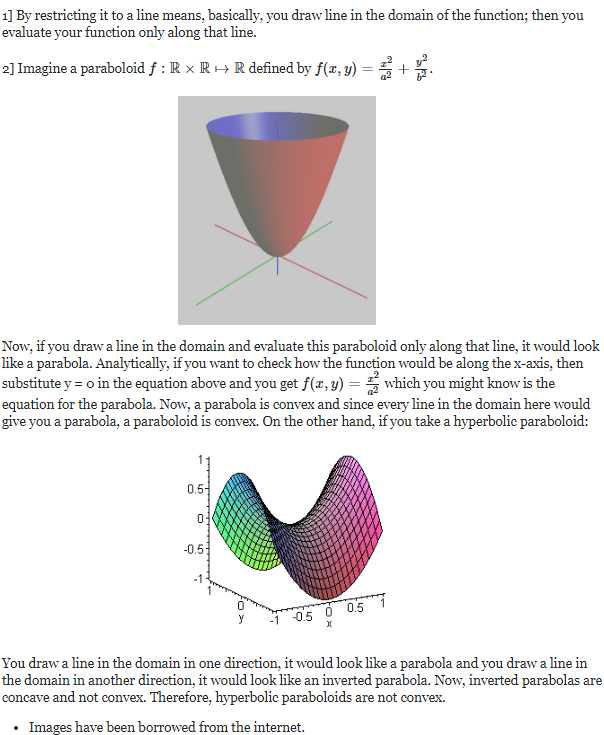
특정 함수가 하나 있다고 해보자.
domain 에서 하나의 점을 찍고, 그 점에서 하나의 방향으로 쭉 선을 그었다고 생각해보자. 함수의 단면? 이라고 생각하면 될듯하다.
그 단면이 convex 한가? 를 측정하는것이다.
여기서 domain에 있는 모든 x 에 대하여, 어떤 방향 v 으로 이 동작을 하던간에, 항상 그 단면이 convex 하다면, 그 함수는 convex funciton 이다.

Extended-value extension
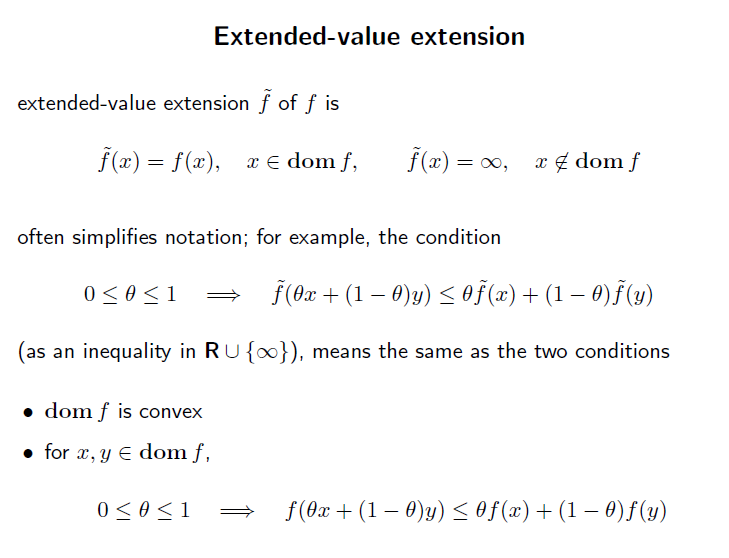
특정 convex function을 모든 실수 공간으로 확장하려한다. 그럴땐 간단하게 기존 함수의 domain이 아닌 영역을 +무한 으로 잡으면 된다. 아래 그럼처럼.
concave function은 반대로 하면 된다.
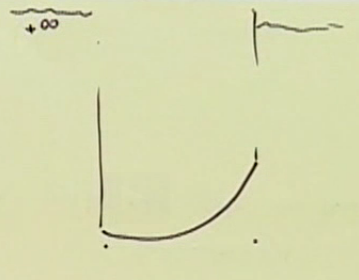
First-order condition
함수 f 가 미분 가능하고, convex function 이라면, 특정 점 x 에서 생성한 1차 테일러 다항식 그래프, R^2 에서 생각해보면 접선은, 항상 그 convex function 보다 작은 함수 이다. global underestimator 이다.

Second-order conditions
함수 f 가 두번 미분 가능할때, matrix에서는 hassian matrix가 존재할때, domain 이 convex 한 함수 f 의 2차 미분이 0 보다 클 경우, 함수 f 는 convex function 이고 그 역도 성립한다.
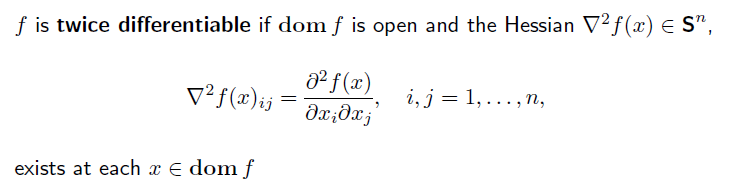
matrix 입장에서는, domain이 convex set 이고, hassian matrix 가 존재하고, hassian matrix 가 positive semi-definite matrix 인 경우, 함수 f 는 convex function 이다.
또한, positive definite matrix 인 경우, strictly convex 이다.

Epigraph and sublevel set
함수 f 가 convex function 일 경우, epigraph 는 convex set 이다.

위 그림은 non-convex function 이므로, epigraph 는 convex set이 아니다. 역도 성립.
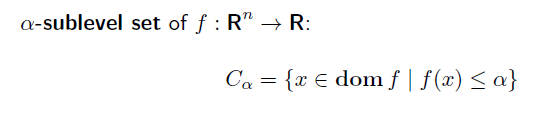
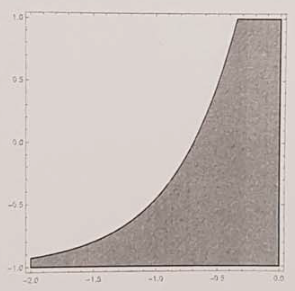
convex funciton 의 sublevel set 또한 convex set 이다. convexity 의 definition을 적용해보면 바로 알 수 있다.
Jensen’s inequality
함수 f 가 convex 이면, f(x) 와 f(y) 의 평균, 또는 line segment 중 하나의 값은, 그에 대응하는 f(x + y) 보다 항상 크거나 같다. 아래 그림을 보면 이해가 될듯.
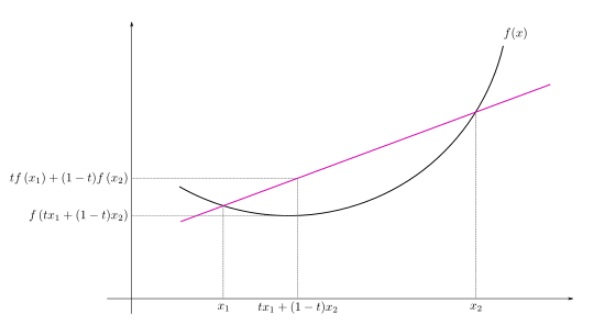
또한, 아래 부등식도 만족한다.
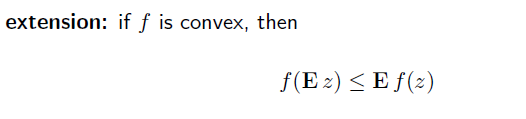
Operations that preserve convexity
convex funciton의 convexity를 유지하기 위한 연산을 살펴보자.
Positive weighted sum & composition with affine function

- convex function에 non-negative 상수를 곱해도 convex function 이다.
- 두 convex function을 합하여도 convex function 이다.
- domain 에 affine function을 적용해도, convex function 이다.
Pointwise maximum
두 convex function max 만 뽑은 function 또한 convex function 이다.
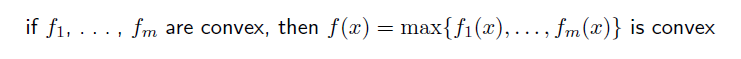
두 convex function의 교집합 이라고 생각됨.
Pointwise supremum
??? supremum에 대한 이해가 없어서 추후 추가 예정…
Composition with scalar functions
g: Rn → R1 인 함수와 h: R → R 인 함수 를 합성해보자.
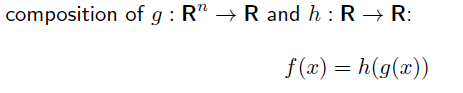
다음과 같은 경우 f 가 convex funciton 이다.
- g 가 convex, h 가 convex, h 의 extended-value extention 이 non-descreasing
- g 가 concave, h 가 convex, h 의 extended-value extention 이 non-increasing
예시)