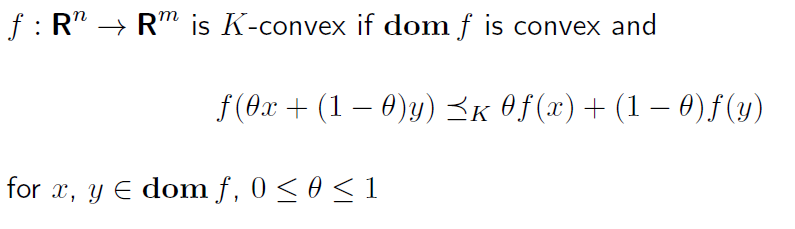Create time: Feb 09, 2020 12:23 PM Update time: Feb 09, 2020 7:33 PM
Lecture 3에서 진행하던 operations that preserve convexity 중 안한거 부터 진행.
Vector composition
g: 실수 n 차원 → 실수 k 차원 함수와 h: 실수 k 차원 → 실수 1 차원 함수가 있다고 해보자.
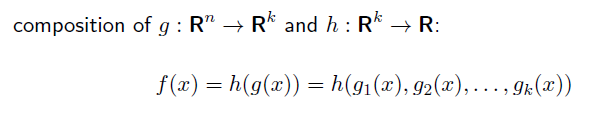
두 함수의 합성함수는 다음 경우에서 convex 이다.
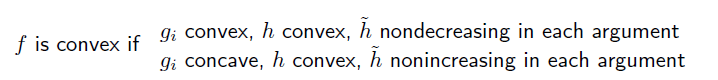
Minimization
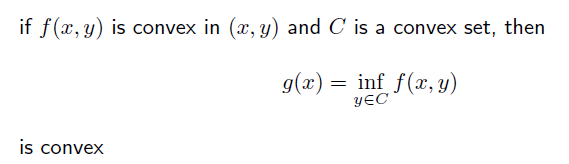
convex function의 minimum 과 infimum은 convex function 이다.
Perspective

convex function의 perspective function 는 convex function 이다.
example
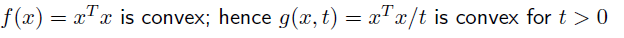
convex function에 양수 scalar를 곱해도 convex function 이므로 perspective of function 도 convex function 이다.
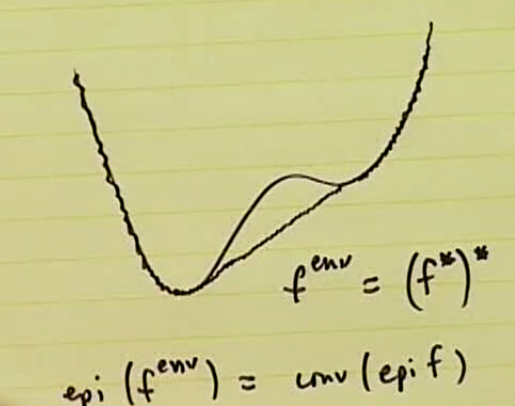
The Conjugate function
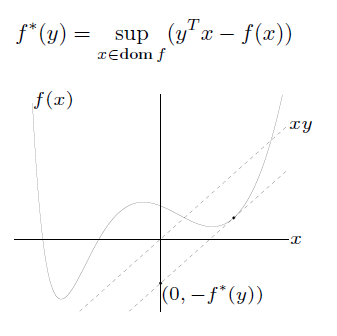
Conjugate 는 함수 f 와, 선형 방정식과의 차이의 supremum 으로 나타내진다.
이떄 f 의 convexity와 상관 없이, f* 은 convex function 이다.
example
negative 로그 함수
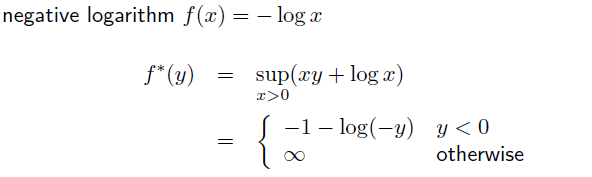
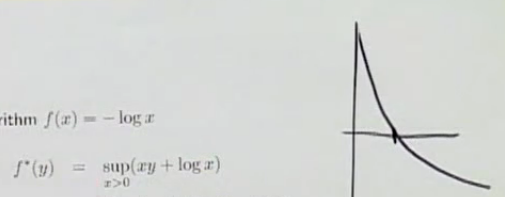
기울기가 음수라면, -logx 아래로 선형 함수가 지나가기 때문에 구할 수 있지만,
기울기가 non-negative라면, -log x 보다 큰 지점이 있어 +무한대가 된다.
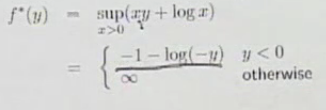
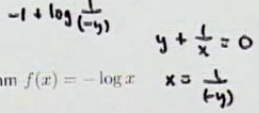
Quasiconvex functions
함수 f 의 domain 과 모든 sublevel set S_a 가 convex 라면 이 함수를 quasiconvex 라고 부름.
만약 함수 -f 가 quasiconvex 라면, f 는 quasiconcave 이다.
f 가 quasiconvex 이고, quasiconcave 라면, quasilinear 라고 부른다. 이 함수의 모든 domain 과 모든 sublevel set 은 convex 하다.
convex function은 quasiconvex function 이지만, 그 역은 성립하지 않는다.
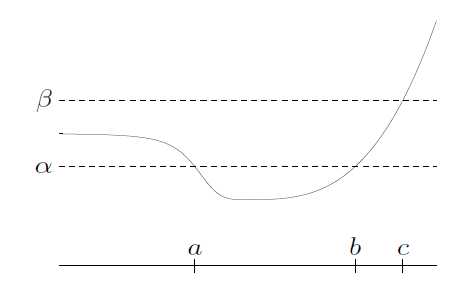
아래 예시들.



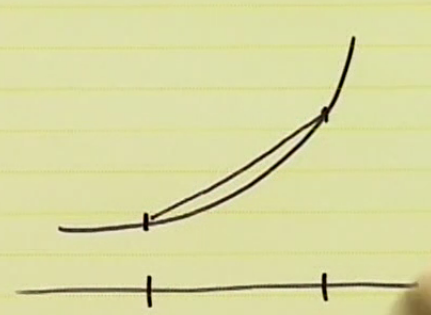
Basic properties of quasiconvex
Modified jensen’s inequality
기존 Jensens’s inequality 는 아래 내용이다.
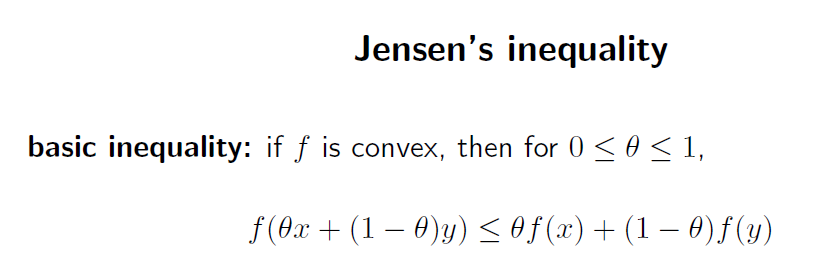
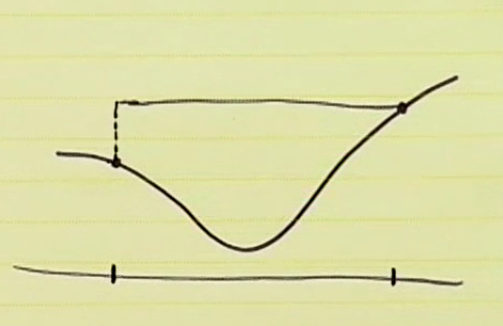
quasiconvex 에서는 조금 변형된다. 두 값의 max 보다 항상 함수값이 작거나 같다.
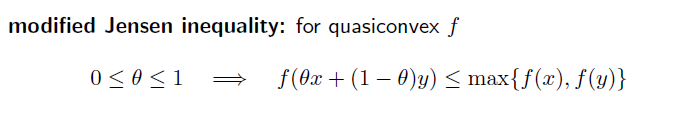
First-order condition
연속 함수 f 가 quasiconvex 라는것은, 다음 조건중 적어도 하나를 만족한다는것이다.
- f is non-decreasing
- f is non-increasing
또한, domain 이 convex 이고, 다음 조건을 만족하면 f 는 quasiconvex function이다.
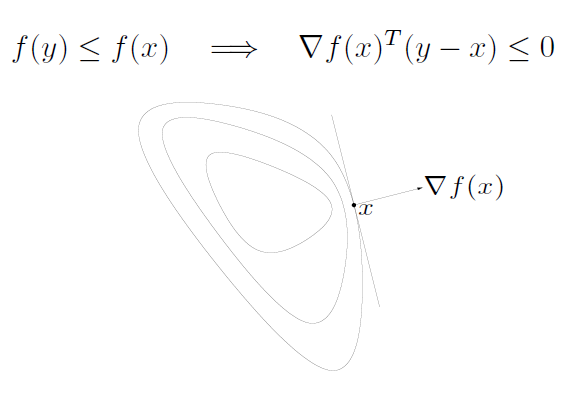
기존 convex function 의 first-order condition 과 유사하게, 특정 지점x 에서의 접선, support hyperplane 을 형성 한다. 왼쪽 오른쪽으로 공간을 나눠주는것을 알 수 있따.
하지만 하나 다른 점이라면, 미분값이 0이 되는 점 x 가 global minimizer 가 될 수 없다는것이다.
Sum
quasiconvex function을 더해도, 반드시 quasiconvex function이 되는것은 아니다.
Log-concave and log-convex functions
log-concave 와 log-convex 의 정의는 다음과같다.
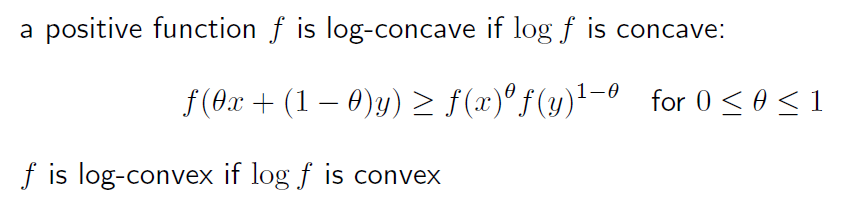
모든 domain x 에서 f(x) > 0 이고, log form 에서 concavity 를 만족하는 경우, log-concave funciton 이라고 부른다.
위 조건에 log 를 씌워보면 명확히 보인다.
보통 log-convex 보다 log-concave 를 많이 사용한다고 한다. 그 이유로는 우리가 알고있는 수 많은 probability distribution function들이 대부분 log-concave function 이기 때문이라고 한다.
Example
Affine function

cumulative gaussian distribution function은 다음과같이 나타난다 함.

여기서 log 를 취하면, 아래 모양처럼 나온다함. 0에 가까울수록 - 무한대 이므로..

Properties of log-concave functions
f 가 두번 미분 가능하고, domain of f 가 convex 인 log-concave function은 다음 식이 성립한다.

Product of log-concve function
항상 log-concave function이 된다. 왜냐하면, log 를 곱하면 더하기이고, 두 concave function 을 더해도 concave function 이기 때문.
Sum of log-concave function
두 log-concave function 의 합은 항상 log-concave function이 되는것은 아니다.
integration
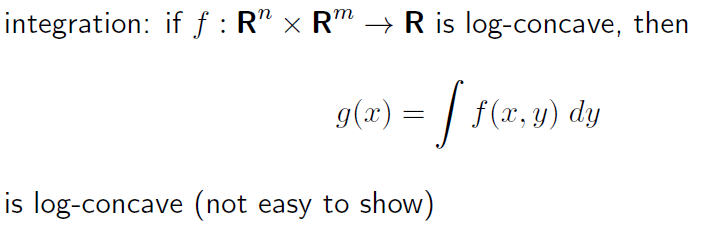
특정 경우에는 log-concavity 도 integration 이후에 보존될 수 있다.
증명이 쉽지 않다고 함.
consequences of integration property
이를 토대로, log-concave probability density 의 marginal distribution 이 log-concave 임을 알 수 있고, convolution 연산에서도 log-concavity 는 닫혀있음을 알 수 있다.
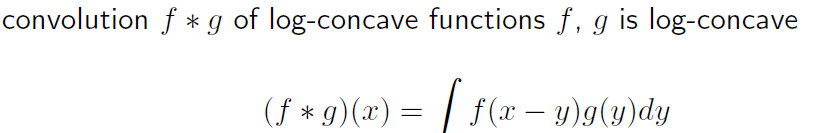
Convexity with respect to generalized inequalities
2장과 3장에서 배웠듯이, R 공간이 아닌 공간에서는 Cone 을 이용하여 inequality를 표현한다.
이번에는 Cone 을 사용하여 R 공간 이외에서도 확장되는 monotonicity 와 convexity 의 개념을 공부해보자.
proper cone K 가 있다고 가정해보자.
K-nondecreasing 은 다음과같이 정의된다.
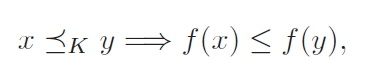
Convexity를 생각해보면, convex domain 상에서 non-decreasing 은, f’(x) ≥ 0을 의미한다.
이를 확장해보면 monotonicity 를 표현할 수 있다.
convex domain 이면서 미분 가능한 함수가 K-non-decreasing 하다는것은, 아래 수식을 만족한다는것이다.
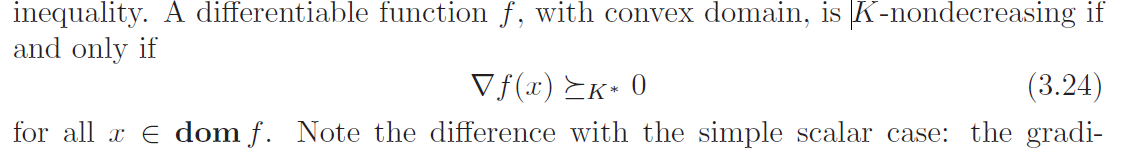
proper cone K 에서 미분값이 항상 0보다 크다면, 이를 K-increasing 이라고 한다.
Proper cone K 에서 domain 이 convex 이고, 아래 수식을 만족한다면, 그 함수를 K-convex 라고 한다.