Create time: Feb 15, 2020 11:40 AM Update time: Feb 16, 2020 11:31 PM

objective function이 위와같은 꼴을 가질때 linear fractional program 이라고 함.
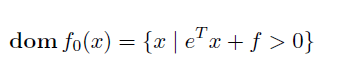
이떄, objective function 의 domain 은 위와같이 분모 > 0 임.
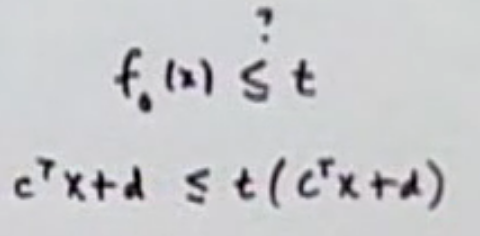
그리고, 이 objective function은 quasiconvex function임. quasiconvex 를 나타내는 부등식에 분모를 양변에 곱하여 비교해보자.

linear fractional program 은 feasible set 이 non-empty 라면, LP 로 변환할 수 있음.
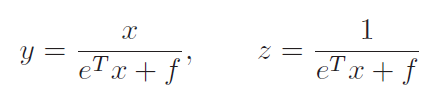
y 와 z 를 다음과 같이 선언함. 그럼 objective function은 아래와 같이 변환됨.
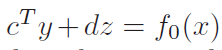
결국 원 domain x 는 위 식으로 치환되어 풀리게됨.

linear-fractional program 을 generalize 한 형태. 여러개의 quasiconvex function의 pointwise maximum을 구하는것이므로 여전히 quasiconvex 임.
r=1 이면 standraf linear fractional program.

objective function이 quadratic form 이고, constraint funciton이 affine 이면 quadratic program 이라 부름.
기하학적으로 보면, constraint 로 만들어진 polyhedron 형태의 feasible set 위에서, ellipsoid 형태의 objective function 을 minimize 하는 task 이다.

예시.
affine function의 norm 의 square 형태를 minimize 하는 task.
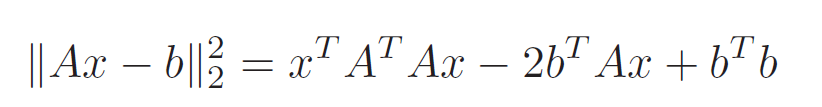
식을 풀어보면 위와같이 quadratic form 이 나옴.

QP 의 constraint funciton이 quadratic form 을 가진다면, quadratically constrained quadratic program 이라고 부름.
이는 feasible set이 intersection of ellipsoid 인 공간에서 ellipsoid 형태의 objective function을 최소화 하는것.

LP 에서 inequality constraint function이 second-order cone constraint 로 바뀌면, Second order cone programming 이라고 함.
standard form
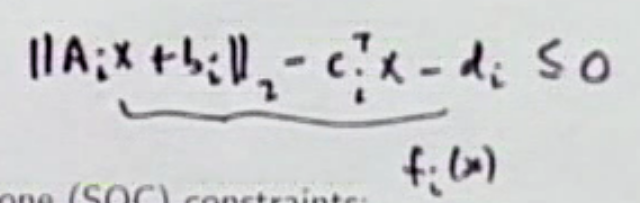

linear programming 에서 parameter 들이 uncertain 한 경우, 어떻게 최적화 할지에 대한 방법이다.
deterministic model 과 stochastic model 이 있음.
- deterministic model
가능한 모든 값을 포함시키는것.

uncertain 한 A 가 위 ellipoisd 영역 어딘가에서 정의된다고 해보자.

가능한 모든 A 가 ellipsoid 안에 있다면, 그럼 AX 의 supremum 이 b 보다 작으면 위 inequality constraint 가 성립할것이다.
이 아이디어를 위 수식으로 풀어내면 최종 형태는 SOCP 형태로 변환됨.
- stochastic model

A 가 특정 probability distrubution 을 따른다고 가정하는것이다.
이번에는 가우시안 분포를 따른다고 가정해보자.
그럼 inequality constraint 를 만족할 경우가 확률을 가질탠데, 이 확률에 confidence score 를 적용한다.
최소한 얼만큼의 확률보다는 믿을만 해야한다 라는 의미로.
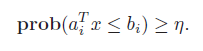
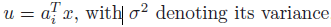
위와같이 변수를 치환하면, 아래 처럼 수식이 변형됨.
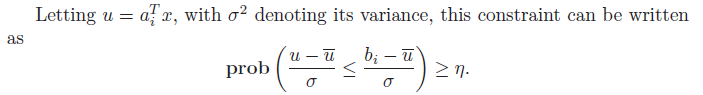
이는 CDF 형태로 나타낼 수 있음. 가우시안 분포의 CDF 는 아래 식.

이제 치환해두었던 variable 들을 다시 복구한다.
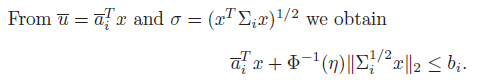
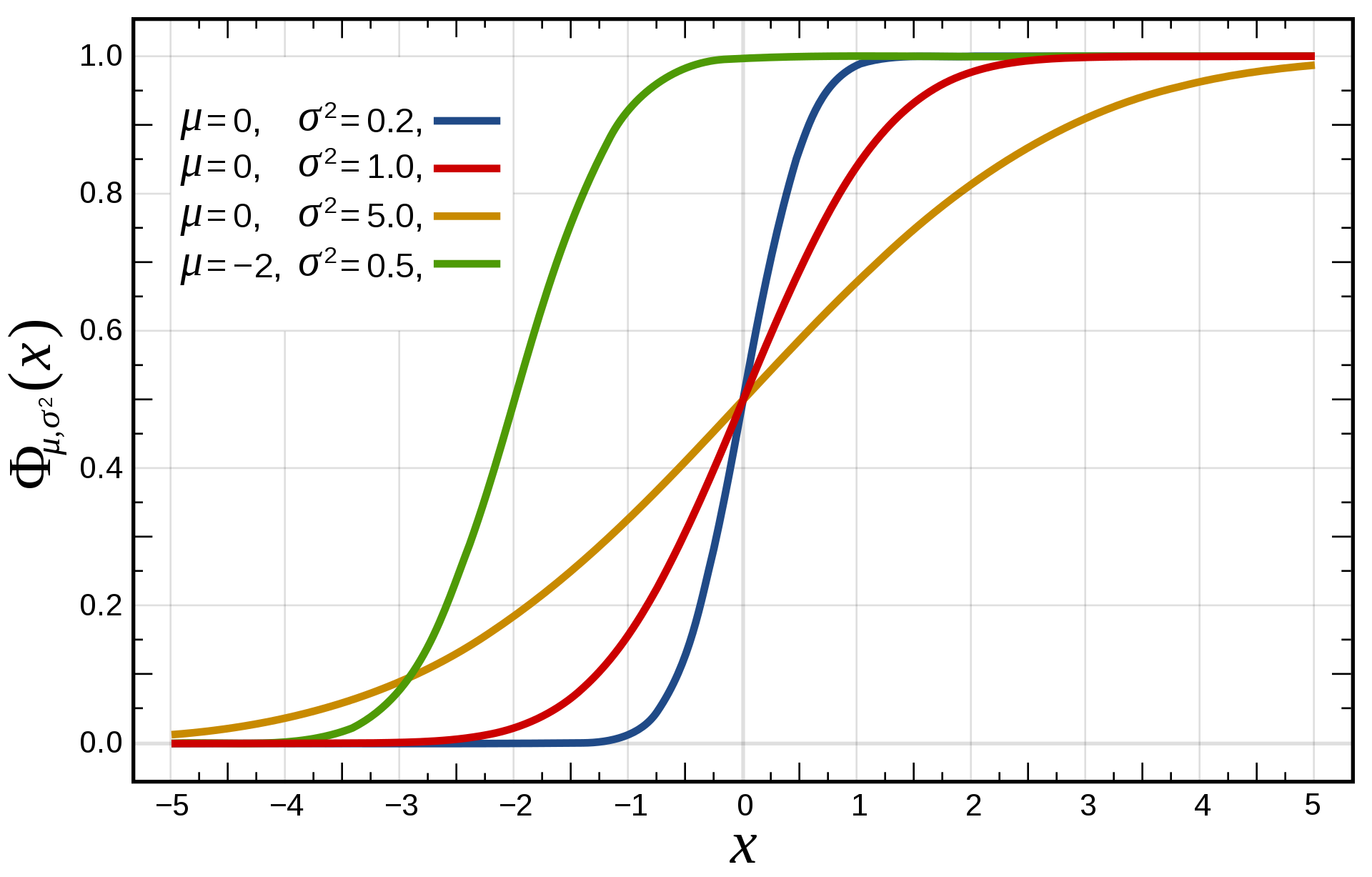
만약, confidence score 가 0.5 보다 크다면, 위 그래프에 따라 아래 수식을 만족함.
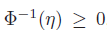
따라서, 이제 robust linear program 을 second order cone program 형태로 변환을 성공하였음.
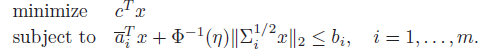


objective function 과 inequality constraint function이 posynomial 이고, equality constraint function이 monomial 인 경우, 이를 geometric program 이라고 부름.
이 geometric program은 보통 convex optimization problem 이 아님. 그러나 convex problem 으로 변환될 수 있음.
새로운 변수 y 를 다음과같이 선언해보자.
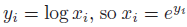
그럼 monomial function은 다음과같이 변환될 수 있다.
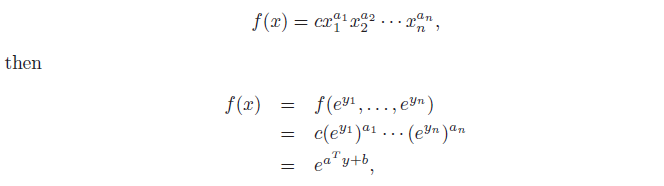
posynomai function은 다음과같이 변환될 수 있다.
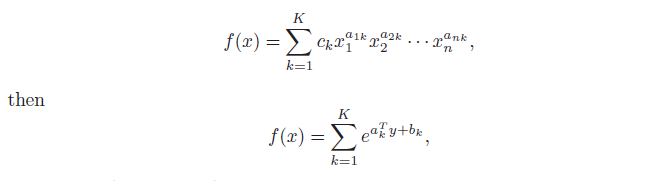
위 두 함수 모두 affine function 형태.
그럼 이제 GP 는 다음과같은 형태로 나타낼 수 있음.
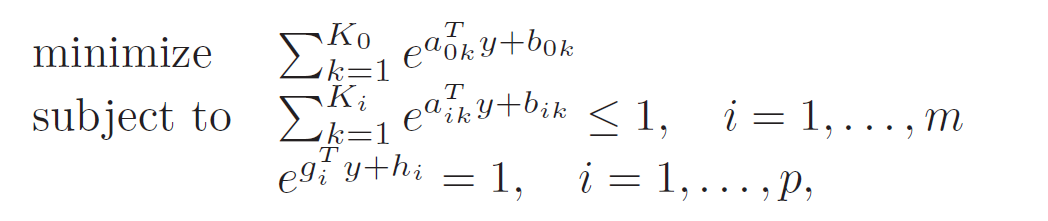
여기에 log 를 씌움.
objective function과 inqeuality function 은 convex function 이고, equality function은 affine function 이므로, convexity 가 유지됨.
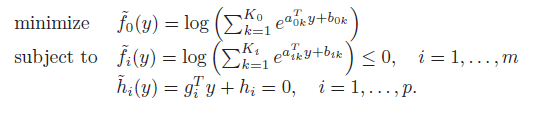
최종적으로 GP 를 Convex problem 형태로 변환.