Create time: Feb 16, 2020 11:46 AM Update time: Feb 16, 2020 11:32 PM

inequality constraint function을 vector valued 형태로 변환하면 이를 generalized inequality 라 부름.
generalized inequality 를 가지느 가장 간단한 convex optimization problem 은 conic form problem 이다.
이는 linear objective function 을 가지고, K-convex한 하나의 affine inequality constraint function을 가진다.
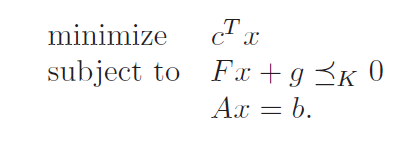

inequality constraint 가 LMI(linear matrix inequality) 형태라면, 이를 Semidefinite program(SDP) 라고 함.
만약 matrix 가 모두 diagonal 형태라면, 각 element 를 분해하여 linear inequality 로 변형시킬 수 있음
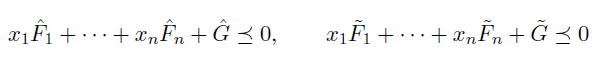
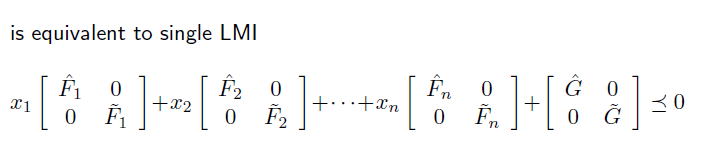

LMI 가 여러개 존재하는 SDP 의 경우, 각 LMI들을 element 로 가지는 큰 matrix 를 구성한다. 이때 이 element 들은 위에서 봤었던 diagonal matrix 형태로 구성한다. 왜냐? diagnoal matrix 형태 구성해야 하나의 matrix 로 합칠 수 있음. 위의 하나의 LMI 를 여러 linear inequality 로 분해하려면 diagonal matrix 여야 했던것과 동일.

다른 여러 문제들을 SDP 로 변형시켜보자. LP 는 diagnoal matrix 형태로 나타내면 되므로 생략.
SOCP 를 SDP 로 변환하는것은 살짝 까다롭다.
이는 schur complement 를 사용하여 식을 변형시켜야 하기 때문. 식을 하나의 block matrix 형태로 변환하는 과정.
- schur complement

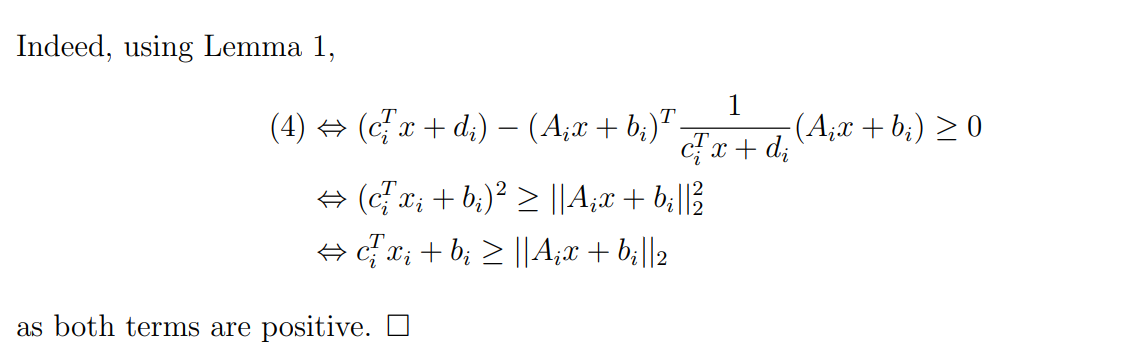
식을 거꾸로 올라가보자.
기존 inequality 를 제곱한다. 여기서 좌측항이 항상 non-negative 이여야 다시 돌아올 수 있음.
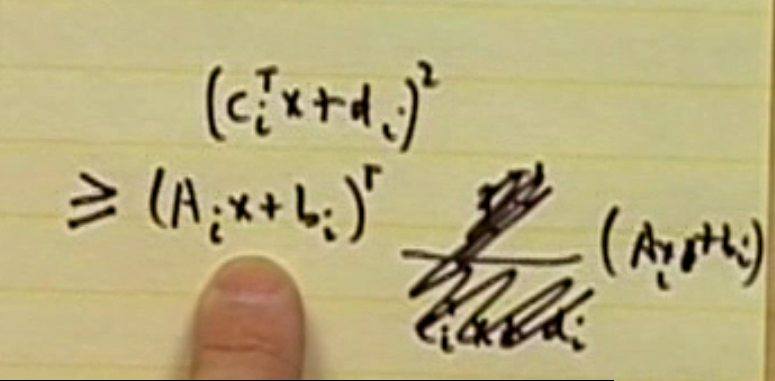
식을 shur complement 형태로 변환. 여기서 A, B, C, D 를 알 수 있음.
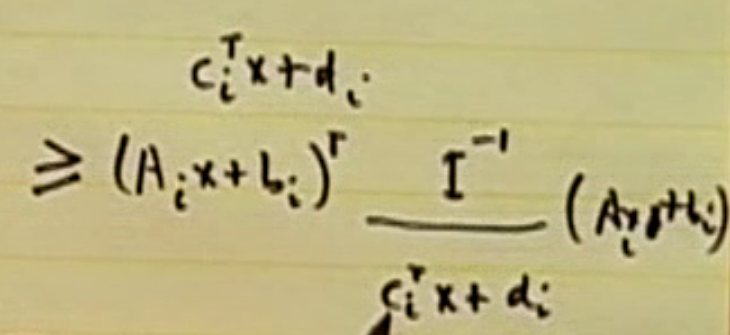
A
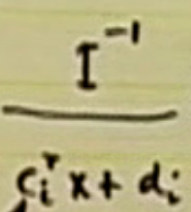
B
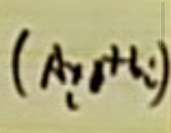
C
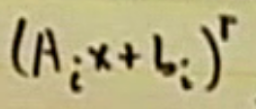
D
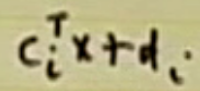

eigenvalue 를 최소화.
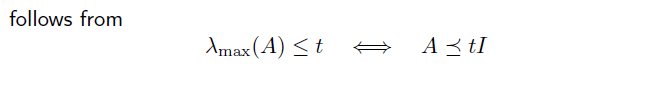
eigenvalue 보다 큰 하나의 값을 설정.
이 값을 minimize 하는 형식으로 SDP form 을 변환.

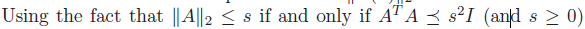
matrix norm 은 위와같이 특정 variable 과의 관계로 나타낼 수 있음.
s 가 non-negative 라면, 제곱을 통해 위의 식으로 변환 가능.

이 식을 또 shur complement로 matrix 형태로 다시 풀어내면, SDP 형태로 변환할 수 있음.

이제 object function 이 vector 공간에서 존재할 수 있도록 해보자.
vector 공간에서 minimize 를 하기 위해서는, 가장 기초적으로 두 value 의 비교가 가능해야함.
이를 위해 cone 을 사용.
K-Convex cone 위에서 두 vector 를 비교하는것은 가능. 따라서 objective function은 k-convex 한 fucntion 이여야 minimize할 수 있음.

feasible set에서 minimum value 가 존재한다면, 그 x 는 optimal.
feasible set 에서 minimal value 가 존재한다면, 그 x 들은 pareto optimal

multicriterion optimization은 여러개의 object function을 가지고있음. multi-objective optimization problem 이라고도 불림.
F1~Fq 는 각각의 다른 scalar objective function.
만약 x, y 가 feasible set 에 있고, x 가 y 보다 좋다(better) 라면, f_i(x) ≤ f_i(y) 을 만족하고, 1~q 중 하나는 f_i(x) < f_i(y) 을 만족한다.

그리고 paretor optimal point 가 있고, feasible y 가 f_0(y) ≤ f_0(x_po) 를 만족하면, 이때는 무조건 f_0(y) = f_0(x_po) 이다.
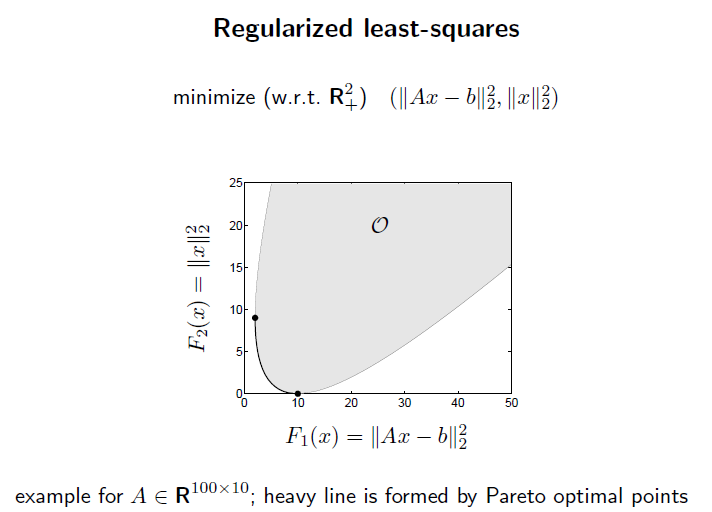

scalarization은 vector optimization problem 에서 pareto optimal 이나 optimal point 를 찾기 위해 사용되는 방법이다.
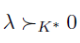
위 조건을 만족하는 하나의 vector를 찾는다. 그리고 feasible set 에서 이 vector 를 방향으로 하는 접선을 만든다.
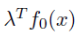
이중에서 최소가 되는 지점을 찾는다. 그럼 almost 대부분의 pareto optimal point 를 찾을 수 있다.
almost 인 이유는 위 그림에서 x_3 같은 영역은 찾지 못한다.
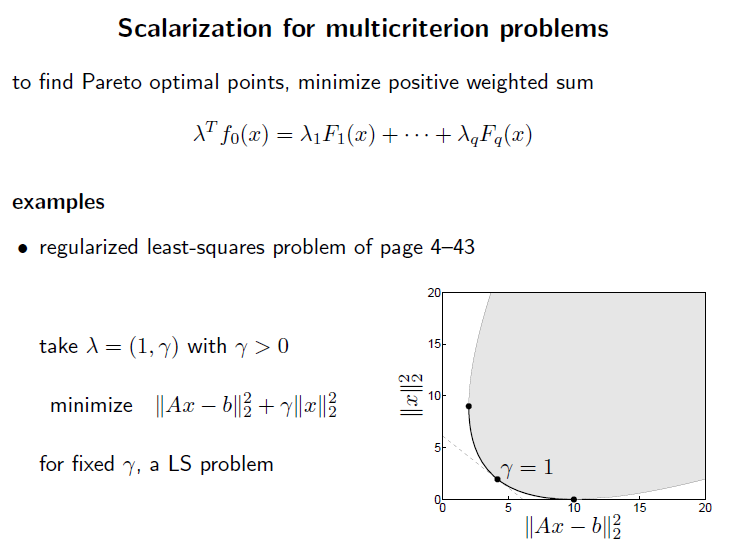
multicriterion problem 에서는 arbiterey 하게 선택하는 람다를 각 objective function에 하나하나 선택하고, 위 식을 다 만족하는 paretor optimal point를 찾는것 이라 생각하면됨.
vector 에서 생각하면 하나의 vector 람다 를 선택하고, feasible set 에서 그 점에서의 접선을 긋는것?. 이 개념은 아직 잘 모르겠다.