Create time: Feb 18, 2020 10:02 PM Update time: Feb 24, 2020 1:24 AM

optimization problem을 바라보는 두 번째 시각인, duality 에 대해 배워보자.

largranian 이란 objective function 과 constraint function을 하나의 다항식으로 합치는 것이다. 그냥 합치는것은 아니고, largrange multiplier vector 를 각 constraint function과 곱하고 합친다. 이 vector 들을 dual variable 이라고 함.

largrangian 을 최소화 하는 것을 lagrange dual function 이라함.
largrange dual function은 lower bound 을 가짐. optimal value 는 아니지만, 특정 조건을 만족한다면 무조건 lower bound 를 보장함.
또한, affine function 을 inf 하는것이므로, concave 함.
관련 증명


LP 를 dual fuction 형태로 나타내보자.
이때 아래 조건을 만족하면, -b^T v 가 최소가 되고, 아니면 음의 무한이 optimal value 가 됨.
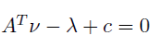
따라서, 위 조건을 만족할때 lower bound 는 -b^T v 임.

위 수식처럼, +- 1 로 constraint 이 걸려있는 함수를 dual function으로 나타내보자.
W+diag(v) 가 semi positive definite 이라면, lower bound 를 정의할 수 있다.

dual function을 conjugate function 형태로 나타낼 수 있음.
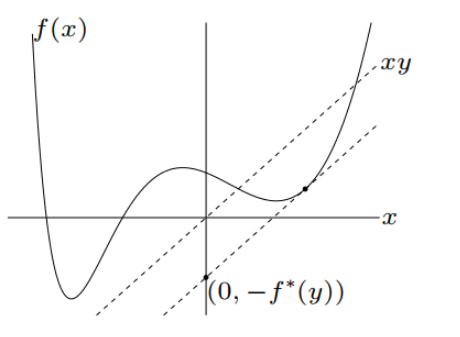

objective function으로 dual function이, constraint function 으로 dual variable 이 오는 것을 dual problem 이라 함.
convex problem 이라함. 이떄 optimal value 를 d, lower bound 를 p로 정의함.

weak duality 는 lower bound 가 optimal value 와 완전히 일치하지 않을 수도 있는상태.
strong duality 는 lower bound 와 optimal value가 완전히 일치하는 상태.
strong duality 는 거의 대부분의 convex problem 에 한함.

strong duality 를 만족하기 위해서는 slater constraint qualification 을 만족해야함.
이는 primal form 에서 각 constraint 에 대한 strictly feasible 한 domain이 존재하면 strong duality 를 가진다고 할 수 있음.

primal form 에서 strictly feasible 한 경우, 즉
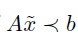
한 경우에 slager’s condition 을 만족하므로, strong duality 를 가짐.
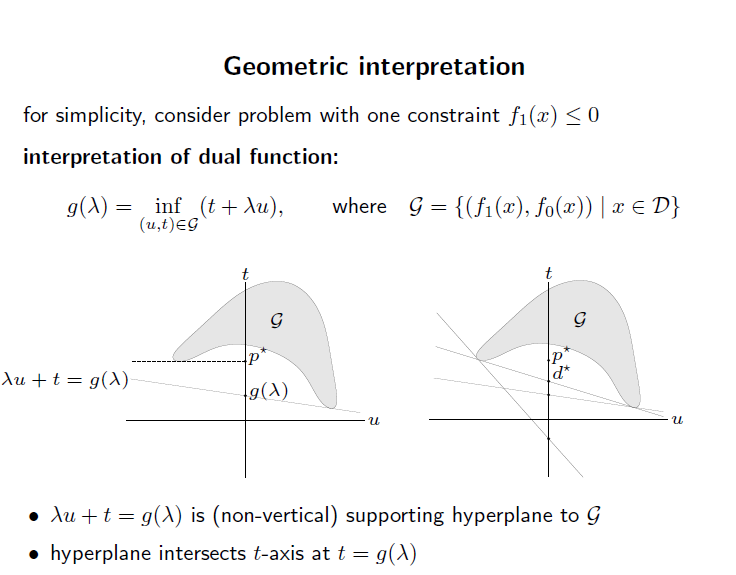
dual problem 을 기하학적으로 살펴보자.
왼쪽 그림에서 아래 constraint 를 적용해보자.
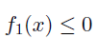
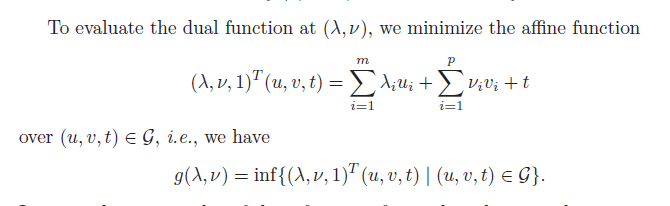
우리가 minimize 할 것은 affine function임.
그럼 lower bound 는 왼쪽 그림의 p* 이 됨.
그리고 g(lambda) 는 위 set 의 hyperplane 이 됨.
dual variable 인 lambda을 조정하면서 lower bound 가 변하는 모습을 알 수 있고, 이게 optimal value 와 동일해질 수 도 있음을 오른쪽 그림을 보면 알 수 있다.
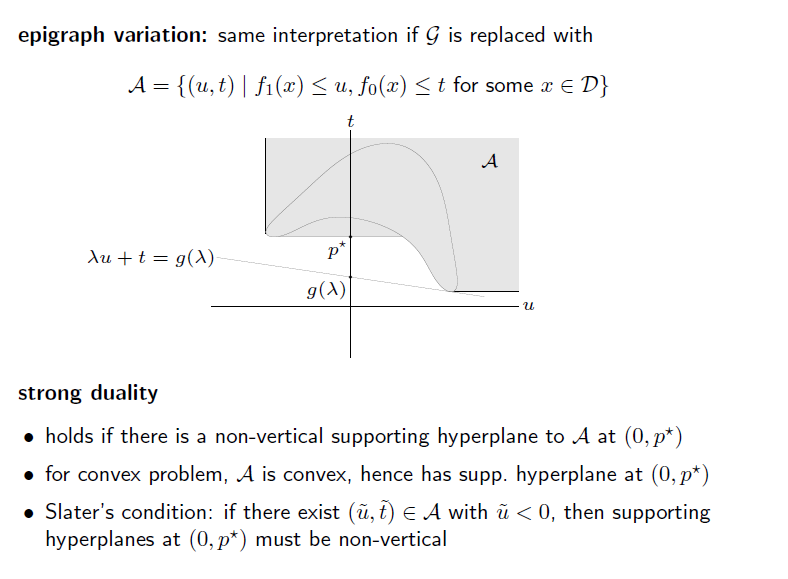
이쪽은 살짝 이해 불가. 흑흑..
