last update datetime: Mar 07, 2020 3:47 PM

머신러닝의 에러는 approximation 과 generalization에서 발생한다.
실제 이상적인 모델과 우리가 학습하는 모델이 있다고 가정해보자.
f 는 이상적인 모델
g 는 학습할 모델
g(D) 는 D 라는 데이터로 학습을 마친 모델
D는 real world 의 데이터
g hat 은 무한한 dataset이 주어졌을때 average hypothesis

만약 우리가 이상적인 모델 f 를 알고있다면, D 라는 데이터가 주어졌을때, 이 모델의 에러를 알 수 있을것이다. 이를 Ex 라고 해보자. Error는 MSE 를 사용한다.
infinite number of datasets, D 가 주어졌을때 expected error는 다음과같다.
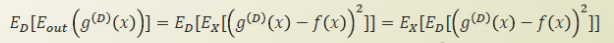
g hat 을 식에 +- 로 추가해서 식을 정리해보자.
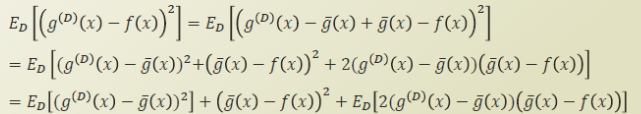
여기서 3번째 항을 생각해보면, D 를 극한으로 보낼 경우, 즉 real world 의 모든 데이터에 대해 학습할 경우, g hat 과 f 는 동일한 함수가 된다. 따라서 3번째 항은 0이 된다.
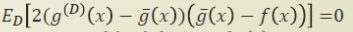
따라서 에러의 기댓값은 다음과같이 정리된다.
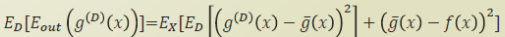

여기서 1항을 variance, 2항을 bias 라고 정의해보자.
variance를 낮추기 위해서는, 결국 더 많은 데이터셋이 필요하다.
그리고 bias 를 낮추기 위해서는 모델을 더 complex 하게 만들어야한다. 하지만 complex 하게 만들경우 overfitting의 위험이 있어 bias 를 낮추기 위해 complex model 을 만들면 variance 가 올라가게되는 trade-off 가 발생한다. 반대도 마찬가지다.
결국 데이터가 중요하다.