1.2 MLE

Files: https://strutive07.github.io/assets/images/1_2_MLE/IE661-Week_1-Part_2-icmoon-ver-1.pdf last update datetime: Dec 29, 2019 8:57 PM

Thumbtack Question

예시) 압정을 떨어뜨렸을때, 앞면일 확률, 뒷면일 확률

5번 던졌을때

• 3번 head
• 2번 tail

이 나왔다고 가정해보자.

Binomial Distribution

discrete probability distribution

N 번의 independent 한 실험을 통해 yes/no 등 2가지 데이터에서 얼마나 많이 두 값이 뜰것인지 에 대한 확률

해당 실험을 Bernoulli experiment 이라고 부름

Independent identically distributed 환경

• 각 실험은 독립적이다.
• 각 실험은 동일한 이산확률분포를 가진다

$$P(T) = \theta, P(F) = 1 - \theta$$

예시)

$$P(TTFTF) = \theta\theta(1-\theta)\theta(1-\theta) = \theta^3 (1-\theta)$$

위 실험을 조금 정리해보자.

Data: TTFTF

횟수 n: 5

True가 나온 횟수

$$a_T = 3$$

True가 나올 확률: theta

theta가 주어졌을때, 위 Data 가 관측 될 확률은?

$$P(Data|\theta) = \theta^{a_T} (1-theta)^{a_T}$$

Maximum Likelihood Estimation

$$P(Data|\theta) = \theta^{a_T} (1-theta)^{a_T}$$

Hypothesis

• 도박의 결과는 theta에 대한 이산확률분포를 따른다.

그럼 hypothesis를 최적화 하는방법은?

• find best candidate of theta
  • 그럼 가장 좋은 후보는 어떻게 찾는가? → MLE

관측된 데이터가 등장할 확률을 최대화하는 theta를 찾아보자!

$$\hat\theta = argmax_\theta P(Data|\theta)$$

해석: P(D

theta)를 최대화 하는 theta를 찾아내고, 그것을 theta hat 이라고 부르겠다.

MLE Calculation

$$\hat\theta = argmax_\theta P(Data|\theta) = argmax_\theta \theta ^ {a_T} (1-\theta)^{\theta_F}$$

지수가 아직 있어서 수식을 처리하기 힘듬.

Log 함수는 monothonic하게 증가하기때문에, log를 식에 추가한다하더라고 최대지점이 변하지 않음.

따라서 이 식에 log를 적용해보자

$$\hat\theta = argmax_\theta lnP(D|\theta) = argmax_\theta ln(\theta^{a_T}(1-\theta)^{a_F}) = argmax_\theta({a_T} ln\theta + {a_F} ln(1-\theta))$$

고등학교로 돌아가보자. 특정 variable에 대해 최댓값은 어떻게 찾았던가?

바로 미분해서 극점을 찾아서 찾았다. 따라서 theta에 대해 미분을 해보자.

따라서, 위 수식을 최대화 하는 theta, 즉 theta hat은 총 등장 수 를 분모로 가지고, a_T 를 분자로 가지는 확률이 된다.

Number of trials

그럼, 5번 던져서 theta = 0.6 이 나온것과, 50번 던져서 theta = 0.6 이 나온것이 동일한것인가?

아니다.

우리가 구한것은, theta hat 이지, theta가 아니다.

즉! 우리는 추론값이다. n이 늘어날수록, 에러가 줄어든다.

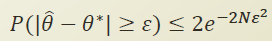
원본 theta와 추론한 theta가 에러 bound 보다 클 확률은, 오른쪽 수식보다 작다고한다.

여기서 N, 즉 trial 값이 parameter로 존재한다.

N 이 커지면 커질수록, error bound가 커질수록, 오른쪽 수식이 작아진다. 즉 error bound 보다 클 확률이 작아진다.

Probably approximate correct(PAC) learning.

• 오차범위 이내에

• 아마도(𝜀) 오차범위(

  𝜃−𝜃∗

  ) 내에서 올바른 결과를 얻을 것이다.