Files: https://strutive07.github.io/assets/images/1_3_MAP/IE661-Week_1-Part_3-icmoon-ver-1.pdf last update datetime: Dec 29, 2019 8:26 PM
MAP: maximum a Posteriori estimation
Incorporating prior knowledge
theta를 구할때, 사전 확률 정보까지 포함해서 확률을 구해보자.

Posterior: D 라는 데이터가 주어졌을때, 특정 theta가 사실일 확률.
Likelihood: 경험
prior knowledge: 사전 확률.
normalizing constant: 데이터.
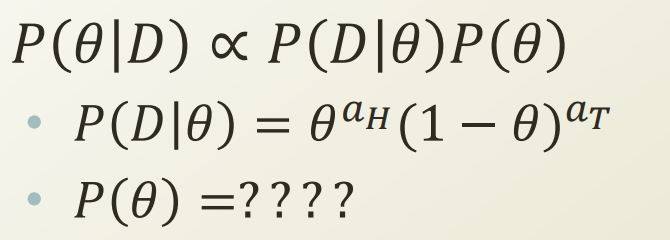
D 는 이미 일어난 사건, 즉 이 사건에 대한 확률은 normalizing constant, 상수 이다. 이 식에서 변하는 값은 theta이므로 D에 대한 확률을 배제하고 식을 바라보자. 상수를 하나 임의로 제거하는것이므로 식이 equal 일 수는 없지만, 비례하므로 수식을 equal에서 비례 로 바꿔준다.
Beta distribution
0에서 시작해서, 1에서 누적 확률값이 1이 되는 distribution
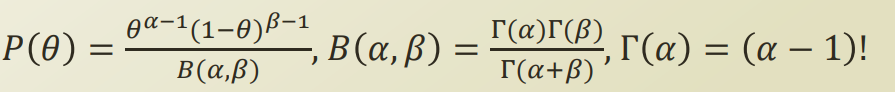
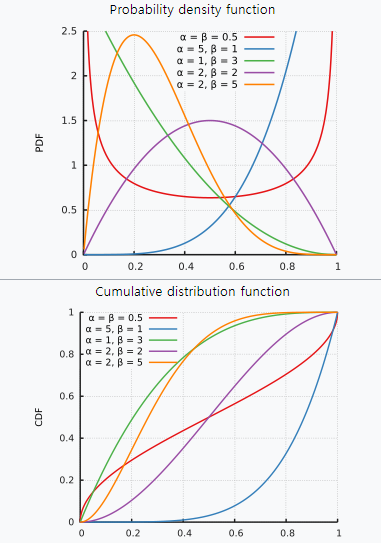
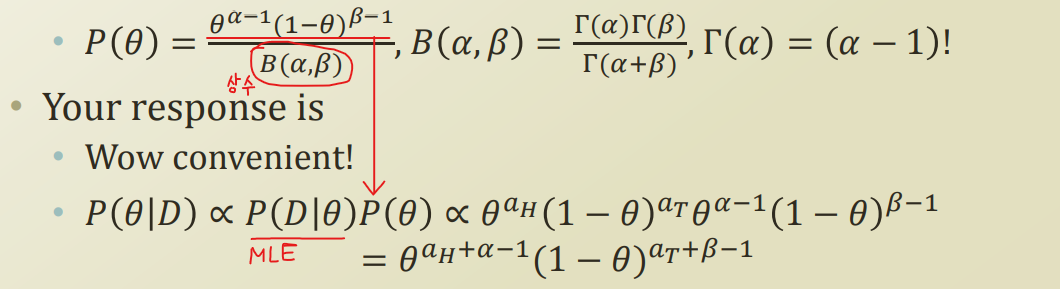
사전확률을 beta distribution 이라고 가정한다면, posterior는 다음과같이 정리된다.
사전확률은 MLE를 공부했을때 처럼, Data와 같이 사전에 준비된 데이터, 즉 상수값이므로 수식을 정리할때 제외하고 수식을 equal 에서 비례로 바꾸면 된다.
Maximum a Posteriori Estimation
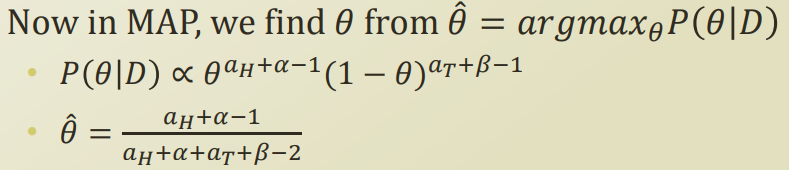
MAP 또한 극점을 통해서 MAP가 최대가 되는 theta를 구하면 위와같이 나온다.
Conclusion from anecdote
그럼 MLE 와 MAP 는 어떤 차이를 가지고 있는것인가?
사실 어느정도 동일한 값이다.
alpha 와 beta 의 값이 무한대 값이 아니라 일반 상수 값이므로, 결국 실험을 계속 할 경우, 즉 a_H 와 a_T 의 횟수가 증가할수록, alpha와 beta의 값은 영향력이 없어진다. 결국 MLE 와 MAP 는 동일한 값이 된다.
하지만, 실험을 많이 하지 못한 상황에서, prior 정보를 기반으로 더 좋거나, 또는 더 나쁜 결과를 가져올 수 있다.
