1.4. Probability and Distribution

Files: https://strutive07.github.io/assets/images/1_4_Probability_and_Distribution/IE661-Week_1-Part_4-icmoon-ver-1.pdf last update datetime: Dec 29, 2019 8:26 PM

Probability

$$P(E) \in R$$

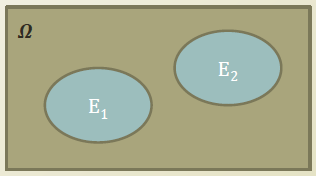
E 는 사건이다.

P(E) 의 값은 R 이라는 continuous value에 속한다.

$$P(E) \geq 0$$

또한, 이럴 경우 P(E) 는 0보다 크다.

$$P(\Omega) = 1$$ $$P(E_1 \cup E_2 ...) = \sum_{i=1}^{\infty}P(E_i)$$

mutually exclusive한 상태에서는 사건의 확률 대한 합집합은 해당 확률의 합과 같다. 교집합이 없는 상태이기 때문이다.

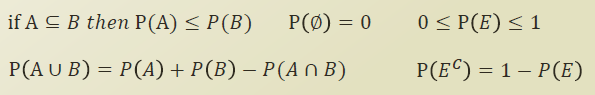
집합이론과도 연관이 있다.

두 확률의 합집합은 두 합에 교집합을 빼는것이고, 확률의 총 합이 1 이므로, 해당 확률의 차집합은 1에서 해당 확률을 뺀것이 된다.

Conditional Probability

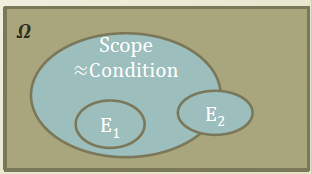
우리는 오메가 라는 전체 사건을 항상 다루지 않는다. 따라서 조건을 두게 된다.

$$P(A|B)$$

조건부 확률은 B 라는 조건이 참일 경우, A 라는 사건이 참일 확률은? 이다.

Probability Distribution

probability distribution이란?

• event 와 확률을 mapping 시켜주는 함수.

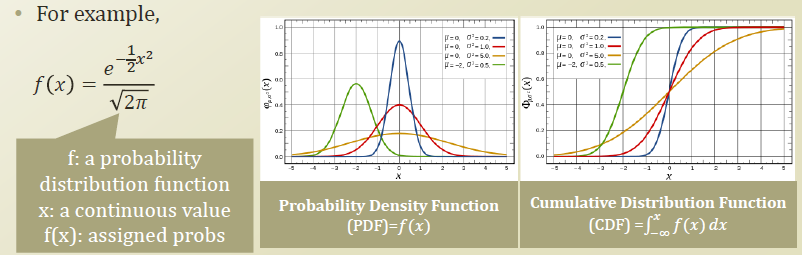
probability distribution function은 위와같이 함수 형태로 나타내진다. 여기에 특정 사건, x 값을 입력하면 x 사건이 발생할 확률이 output으로 나오게 된다.

PDF

• PDF 란, 위에서 봤던 확률분포함수 그 자체이다.
• 확률값은 항상 0보다 크고, 1보다 작다.
• 함수 확률값의 총 합은 항상 1이다.

CDF

• CDF 란, 위 PDF 를 누적한 분포이다.
• x 라는 사건이 있을때, CDF 의 output은, 음의 무한대 부터 x 까지의 pdf 확률 값의 합 이다. 위 ppt에서 적분 형태로 나타낼 수 있다.
• 이 함수의 양의 무한대는 항상 1이다.

Normal distribution

가장 많이 사용되는 distribution 이다.

$$f(x;\mu,\sigma) = \cfrac{1}{\sigma \sqrt{2\pi}}e^{-\cfrac{(x-\mu)^2}{2\sigma^2}}$$

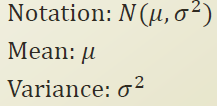
mean 과 variance 라는 parameter를 가지는 확률분포이다.

PDF 는 다음과같은 형태를 가진다.

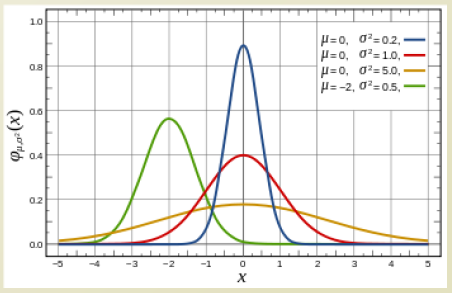
normal distribution은 분포 양 끝에 0으로 점점 수렴하는 long tail을 가지고 있다.

CDF 는 다음과 같은 형태를 가진다.

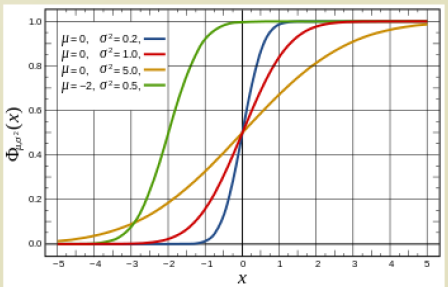
Beta distribution

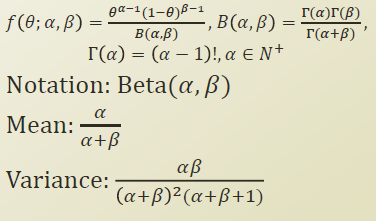
beta distritubion은 알파와 베타 라는 두 parameter를 가진다.

PDF 는 다음과 같은 형태를 가진다.

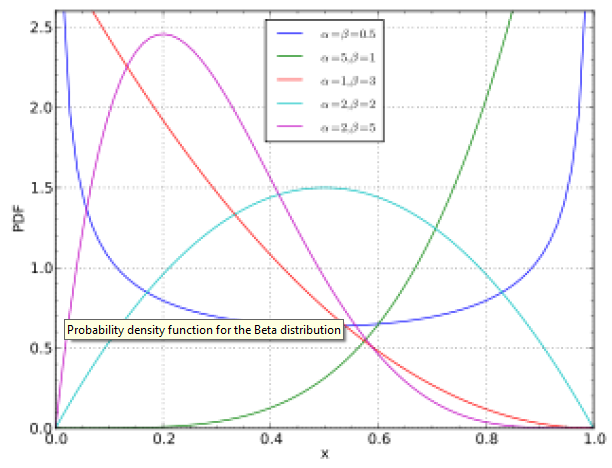
normal distribution과 다르게, long tail이 없고, 사건의 범위 [0, 1]로 명확히 정해져있다.

CDF 는 다음과 같은 형태를 가진다.

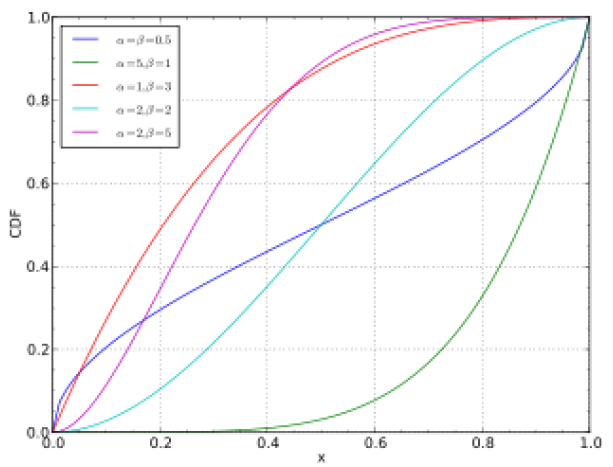
Binomial distribution

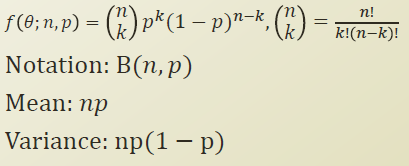
이항분포는 사건이 True, False 로 2가지 사건만 존재할 때 사용한다.

n번의 연속된 독립시행에서 각 시행이 p 만큼의 확률을 가질때 사용할 수 있는 확률분포이다.

n 은 횟수이고, p 는 해당 사건이 참일 확률이다.

n=1 일때 이항분포는 베르누이 분포와 같다.

PDF 는 다음과같은 형태를 가진다.

위 두 distribution과 다르게, discrete 한 event 에 대한 확률 분포를 정의할 때 사용하는 분포이다.

CDF 는 다음과 같으 형태를 가진다.

Multinomial distribution

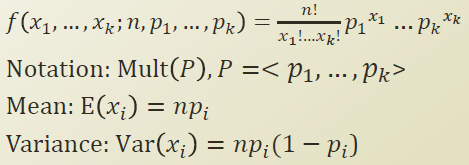
binomial distribution을 일반화한것으로, 여러개의 true, false 에서 벗어나 여러가지 사건이 있을 수 있다.

이외에도 여러가지 distribution이 있다.