last update datetime: Mar 07, 2020 1:11 PM

primal form → dual form 으로 변환 한 경우, lower bound == optimal point 임을 보장하려면, 특정 조건을 만족해야한다.
convex optimization 에서는 slater’s constraint qualification 을 만족해야한다고 했는데, 여기서는 karush-kunh-tucker(TTK) condition 이라는것을 만족해야한다고 한다.
(8강까지 듣고왔는데 이게 9강에서 나오는듯하네 이런~)

위와같이 KKT condition 을 만족해야함. 증명은 convex optimization 강의에서 배워보자.

자 그럼 SVM 식을 dual problem 으로 변형해보자.
equality constraint function은 없고, inequality constraint function만 있으니, lagrange maltiplier 는 알파 하나 이다.
이를 식에 적용하자.
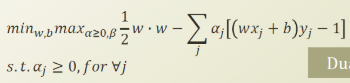
그리고 KKT condition을 계산해둔다.
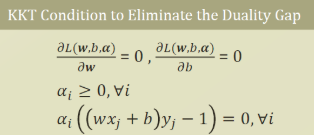
미분을 하면 아래와같이 변형된다.


이제 object function을 dual function으로 변형시키자.
여기서 KKT condition의 조건을 대입하면, 위와같이 식을 변형시킬 수 있다.,
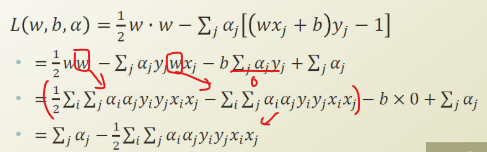
최종 function 을 보면, 알파에 대한 quadratic problem 으로 변형된 것을 알 수 있다.

일단 우리는 non-linear 속성을 SVM 에 부여하기 위해서는, 차원을 늘리는수 밖에 없다.
하지만, 차원을 늘리면 feature space 가 매우 커지고, 계산량이 너무 많아진다. 내적이라도 한번 들어간다면 엄청난 연산을 견뎌야할 것이다.

이 연산량을 줄이기위해 Kernel function이 사용된다.
특정 조건을 만족하는 kernel function 을 적용한다면, 두 값을 내적하고 다른 차원으로 보내는것과, 다른 차원으로 보낸 후 내적 하는것이 동일한 결과를 가져온다는것이다.

polynomial kernel function에 대한 예시.
따라서, 고차원 매핑과 내적을 하나의 kernel function에서 매우 빠르게 계산할 수 있게 된다.
해당 조건에 대한 설명

이제 다시 dual problem 으로 넘어와보자.
dual problem 에서 non-linear 속성을 부여하려면, 위와같이 고차원 매핑이 필요하다.
하지만 여기서 고차원 매핑을 하고 내적한것은, kernel function과 동일한것이므로, kernel function으로 대체할 수 있다.
또한 x는 최적화할 대상이 아니므로 미리 모두 계산해두고 optimization할때 constant 한 값으로 사용할 수 도 있다.
그럼 여기서 W 는 어떻게 구할까? W 는 내적이 아니라 kernel function을 사용하지 못하는것 처럼 보인다.
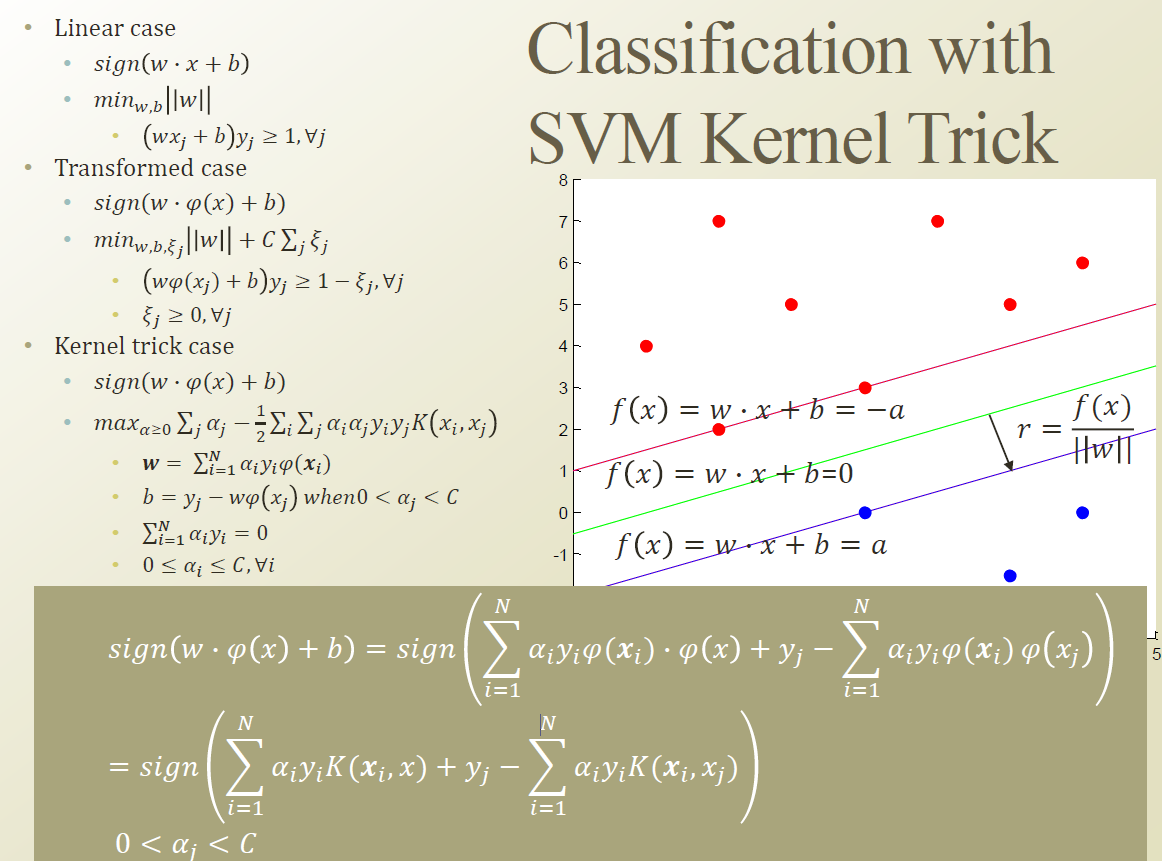
하지만 여기서 최종 결과물을 보면, 결국 W 에 x 를 내적하는것이므로, 이를 kernel function으로 치환하여 문제를 풀 수 있다.
kernel function을 사용한다면, w 와 b 에 대해 의미를 쉽게 부여할 수 는 없지만, 아무튼 classification 은 할 수 있게 된다.
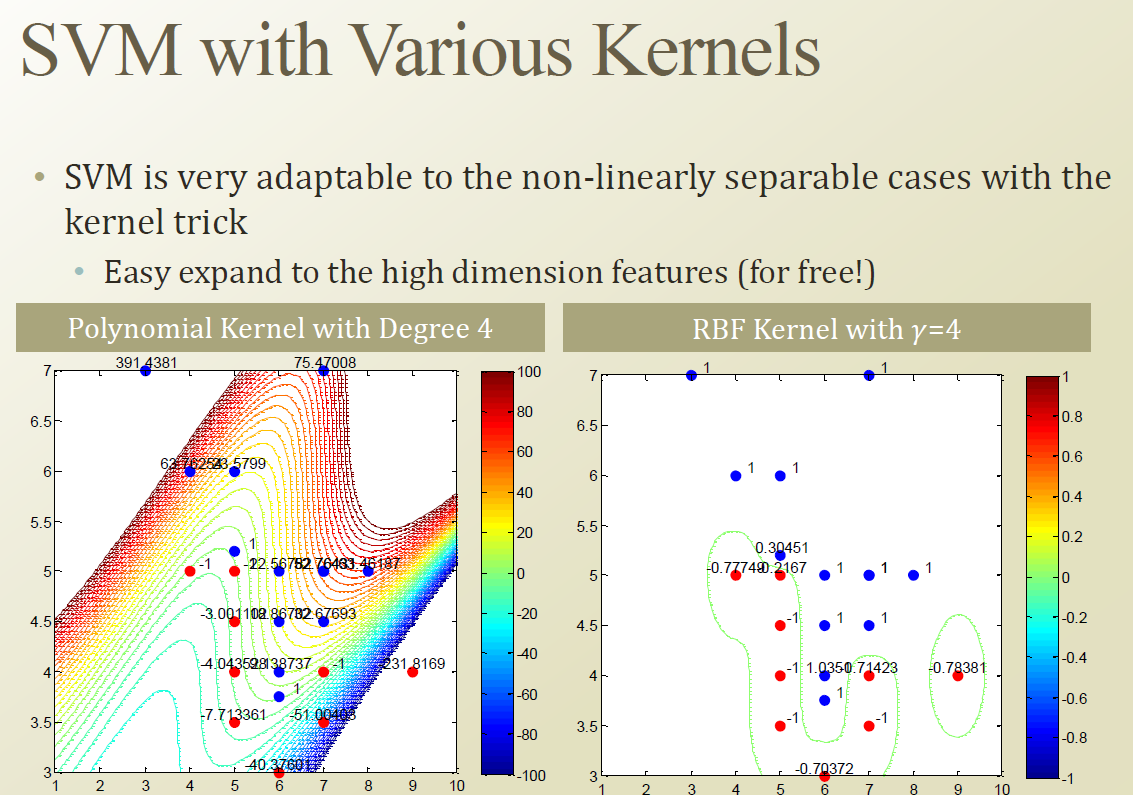
다양한 kernel funciton을 자기 문제에 맞게 사용할 수 있다.